Calculation of the option price for European call options
Case directory
$FOAM_TUTORIALS/financial/financialFoam/europeanCall
Summary
The Black-Scholes equation will be solved to determine the option price of a European call option (an option exercisable only on the maturity date). The Black-Scholes equation for a call option is generally written as a partial differential equation as follows.
where t is time, V is the option price, S is the stock price, σ is the volatility, and r is the risk neutral rate.
The meshes are as follows. The meshes has only one layer in the Y and Z directions and the solution is obtained as a solution of one-dimensional model.
Meshes
The results of the calculation are saved under the graphs directory for each time period, as shown below.
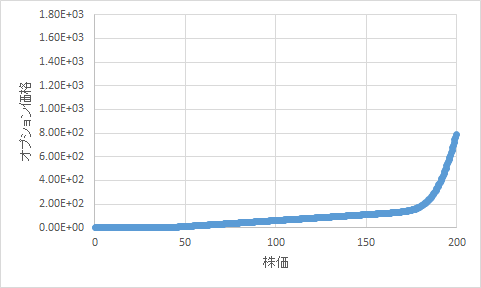Option price at time 0.1 (V)
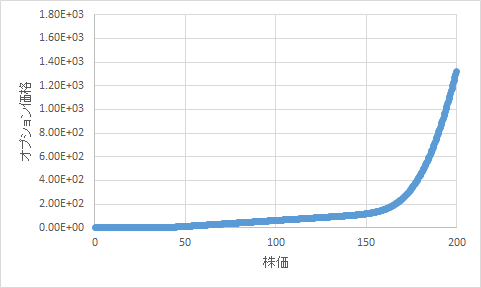Option price at time 0.3 (V)
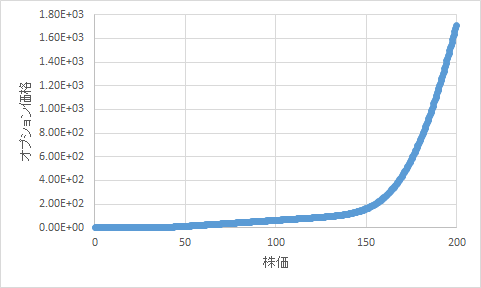Option price at time 0.5 (V)
Commands
cd europeanCall
blockMesh
financialFoam
gnuplot
gnuplot>plot "graphs/0.5/V.xy"
In the example above, we use gnuplot to graph the option price (V) at time 0.5.
Calculation time
0.42 seconds *Single, Inter(R) Core(TM) i7-2600 CPU @ 3.40GHz 3.40GHz