Flow around an obstacle of a porous media
Case directory
$FOAM_TUTORIALS/incompressible/pisoFoam/laminar/porousBlockage
Summary
We calculate the flow around a porous body obstacle placed in a uniform flow from 0 sec to 100 sec. We solves the Navier-Stokes equations directly without using a turbulence model.
The obstacle is defined as a cell zone "porousBlockage". The fluid flow in from region "inlet" at (1, 0, 0) m/s and out from region "outlet". A symmetry condition is set for the region symmetryPlane, which is the upper and lower surface in the Y direction. The problem will be solved as 2-dimensional problem with a single mesh in Z direction.
 Model geometry
Model geometry
Porous media depends on the Darcy-Forchheimer law 
porosity1
{
type explicitPorositySource;
active yes;
explicitPorositySourceCoeffs
{
selectionMode cellZone;
cellZone porousBlockage;
type DarcyForchheimer;
D 1000;
DarcyForchheimerCoeffs
{
d ($D $D $D);
f (0 0 0);
coordinateSystem
{
type cartesian;
origin (0 0 0);
coordinateRotation
{
type axesRotation;
e1 (1 0 0);
e2 (0 1 0);
}
}
}
}
}
The meshes are as follows.
 Meshes
Meshes
The calculation result is as follows.
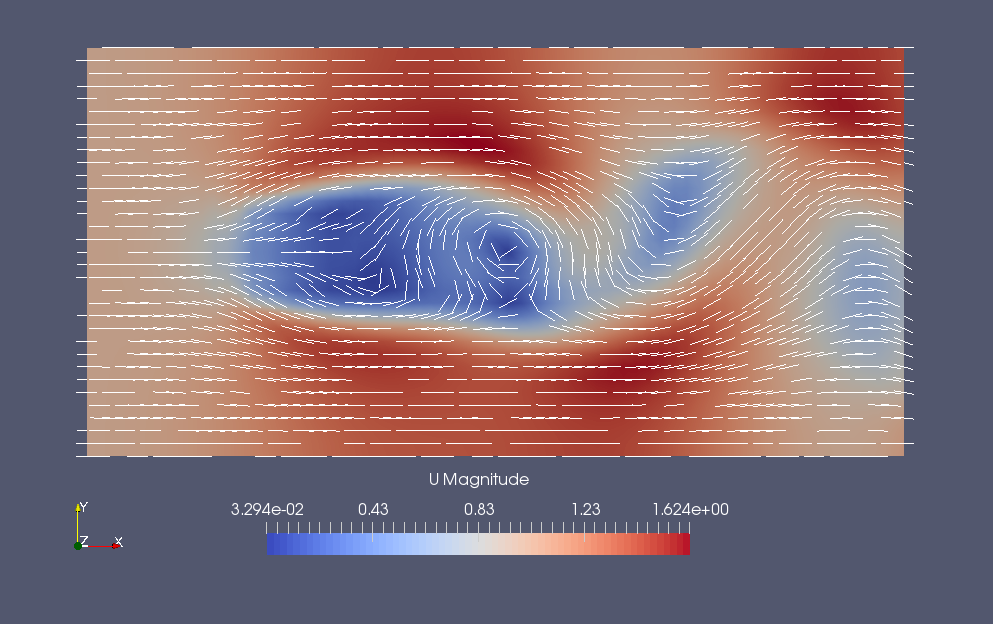 Flow velocity at final time (U)
Flow velocity at final time (U)
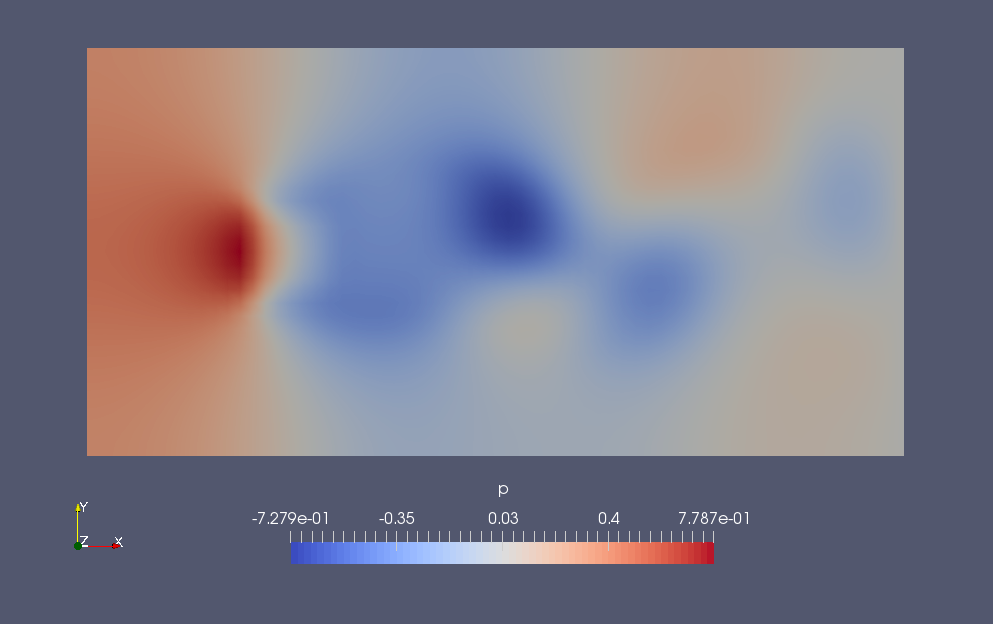 Pressure at final time (p)
Pressure at final time (p)
We can see that the flow is destabilized and a Kalman vortex is generated behind the obstacle.
Commands
cd porousBlockage
blockMesh
topoSet
pisoFoam
paraFoam
Calculation time
11.3 seconds *Single, Inter(R) Core(TM) i7-2600 CPU @ 3.40GHz 3.40GHz