Flow by shallow water equation
Case directory
$FOAM_TUTORIALS/incompressible/shallowWaterFoam/squareBump
Summary
The shallow water equation is used to calculate the flow in a system where the velocity distribution in the depth direction can be ignored. The equations to be solved are as follows.
where h and u are the fluid depth (fluid surface height) and velocity vector, respectively. The f is the Coriolis force, g is the acceleration of gravity, h0 is the deviation from the mean fluid depth, and τω and τb are the stresses from the fluid surface and bottom, respectively.
Fluid flows in from the region "inlet" (red part) at a velocity of (0.1, 0, 0) m/s and out from the region "outlet" (green part). The walls of the channel (blue part) are set to slip wall conditions, and the calculation is performed as a 2-dimensional problem with a single mesh in the Z direction. The fluid depth is set to 0.009 m only in the center of the channel and 0.01 m in the other areas.
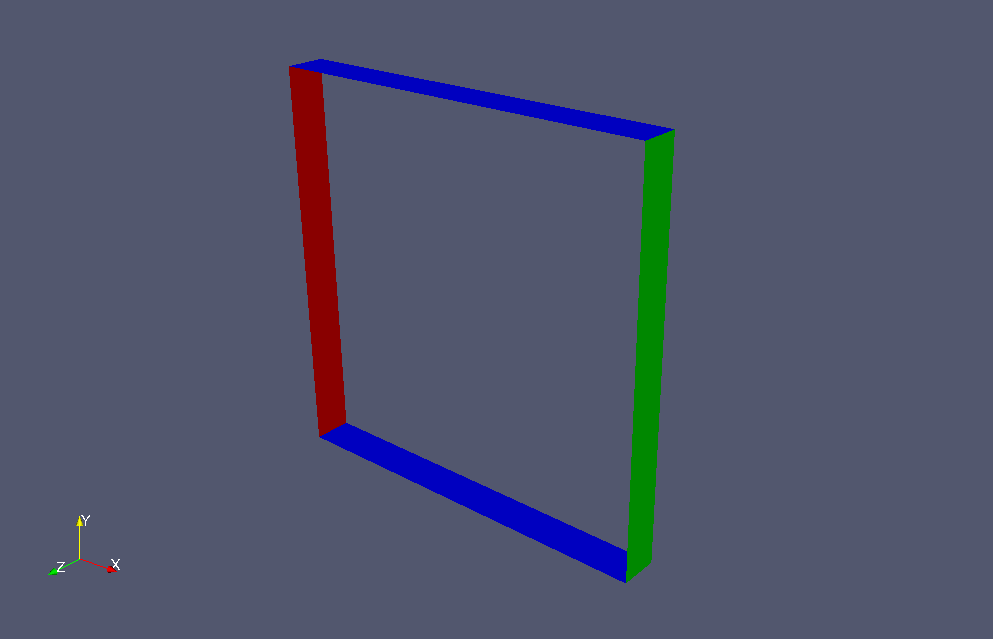 Model geometry
Model geometry
 Definition of fluid depth
Definition of fluid depth
The meshes are as follows.
 Meshes
Meshes
To visualize the fluid depth, Check "h" in the "Properties" tab on ParaView.
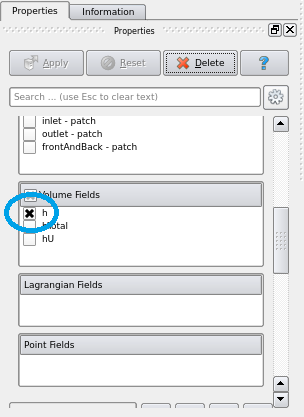 Check h
Check h
The calculation result is as follows.
 Depth distribution of fluid at 0 second (h)
Depth distribution of fluid at 0 second (h)
 Depth distribution of fluid at 1 second (h)
Depth distribution of fluid at 1 second (h)
 Depth distribution of fluid at 100 seconds (h)
Depth distribution of fluid at 100 seconds (h)
We can see how the wave is generated at the central projection and then approaches the steady state.
Commands
cd squareBump
blockMesh
shallowWaterFoam
paraFoam
Calculation time
4.87 seconds *Single, Inter(R) Core(TM) i7-2600 CPU @ 3.40GHz 3.40GHz

