節点・面接触要素はマスター面につながったスレーブ節点で構成されます(図110を参照)。従ってこの接触要素は 1+nm 個の節点で構成されます。ここで nm はマスター面に属する節点の数です。有限要素の剛性行列は各節点での変位については各節点の内力の導関数になります。従って、私たちは節点での内力を決定する必要があります。
スレーブ節点位置を p、そのマスター面への投影位置を q とすると両者を結んだベクトルは以下のようなります。
またこの位置での間隔 r は次のようになります。
| r = r・n | (62) |
ここで n はマスター面上のローカルな法線を意味します。マスター面に属する節点を![]() 、面内でのローカル座標を ξ 、ηとすると、次のように記述できます。
、面内でのローカル座標を ξ 、ηとすると、次のように記述できます。
さらに次の様になります。
| (65) |
m は面のヤコビベクトルです。節点 p での内力は以下の式に従います。
ここで f はユーザーによって選択された圧力と間隔の関数、ap は節点 p に代表されるスレーブ領域面積です。N に属するスレーブ節点が面積 Ai のスレーブ面 i に触れる場合、その面積は以下の様に求められます。
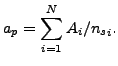 |
(67) |
式(66)のマイナス符号は内力が外力のマイナスであることに由来します(外力とはマスター面からスレーブ節点に働く力です)。式(66)の法線をそのノルムで割ったヤコビベクトルで置き換え、ui で微分(i はスレーブ節点またはマスター面に属する任意節点)すると以下が得られます。
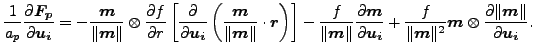 |
(68) |
ここで
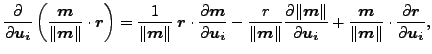 |
(69) |
なので、上記の式は以下の様に書き換えられます。
従って未定の導関数は![]() 、
、![]() 、
、![]() ということになります。
ということになります。
m の導関数は式(64)から得られ、以下の様に書くことができます。
![$\displaystyle \boldsymbol{m}= \sum_j \sum_k \frac{\partial \varphi _j}{\partial...
...partial \varphi_k}{\partial \eta } [ \boldsymbol{q_j} \times \boldsymbol{q_k}].$](img542.png) |
(71) |
これを微分すると以下の様になります(ξ と η は ui の関数であること、![]() であることに注意してください)。
であることに注意してください)。
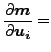 |
![$\displaystyle \left [ \frac{\partial^2 \boldsymbol{q} }{\partial \xi^2} \times ...
...partial \eta } \right] \otimes \frac{\partial \xi }{\partial \boldsymbol{u_i} }$](img545.png) |
|
| + | ![$\displaystyle \left[ \frac{\partial \boldsymbol{q} }{\partial \xi } \times \fra...
...partial \eta} \right] \otimes \frac{\partial \eta }{\partial \boldsymbol{u_i} }$](img547.png) |
|
| + | ![$\displaystyle \sum_{j=1}^{n_m} \sum_{k=1}^{n_m} \left[ \frac{\partial \varphi_j...
...right] (\boldsymbol{I} \times \boldsymbol{q_k}) \delta_{ij}, \:\:\: i=1,..n_m;p$](img548.png) |
(72) |
右辺にある導関数![]() 、
、![]() は未知で、後で求めます。これらは任意の ui が変化したときの ξ と η の変化量を表します。k はスレーブ節点、またはマスター面に属する任意の節点です。ξ と η の値はスレーブ節点をマスター面に正射影して得られることに注意してください。
は未知で、後で求めます。これらは任意の ui が変化したときの ξ と η の変化量を表します。k はスレーブ節点、またはマスター面に属する任意の節点です。ξ と η の値はスレーブ節点をマスター面に正射影して得られることに注意してください。
式(61)と式(63)を組み合わせて r を得ると、ui の導関数は以下の様に書けます。
![$\displaystyle \frac{\partial \boldsymbol{r} }{\partial \boldsymbol{u_i} }= \del...
...rtial \boldsymbol{u_i} } + \varphi_i (1 - \delta _{ip}) \boldsymbol{I} \right],$](img552.png) |
(73) |
ここで p はスレーブ節点を表します。
最終的にベクトルのノルムの導関数はベクトル自身の導関数で書き表すことができます。
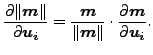 |
(74) |
残るは ξ と η の ui に対する導関数です。q がマスター面に対する p の正射影であるということは接続ベクトル r がマスター面に接するベクトル![]() 、
、![]() と直行するということです。
と直行するということです。
ここで
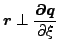 |
(75) |
は以下の様に書くことができます。
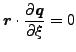 |
(76) |
あるいは次の様に書くこともできます。
![$\displaystyle \left [\boldsymbol{p} - \sum_i \varphi_i (\xi ,\eta) \boldsymbol...
...ft[ \sum_i \frac{\partial \varphi_i}{\partial \xi } \boldsymbol{q_i} \right]=0.$](img558.png) |
(77) |
上式を微分すると次の様になります。
![$\displaystyle \left[ d \boldsymbol{p} - \sum_i \left(\frac{\partial \varphi_i}...
...ta + \varphi_i d \boldsymbol{q_i} \right) \right] \cdot \boldsymbol{q_{\xi }} +$](img559.png) |
||
![$\displaystyle \boldsymbol{r} \cdot \left[ \sum_i \left(\frac{\partial^2 \varph...
...\frac{\partial \varphi_i}{\partial \xi } d \boldsymbol{ q_i} \right) \right] =0$](img560.png) |
(78) |
ここで qξ は q の ξ に対する微分です。上式は以下の様に書き直すことができます。
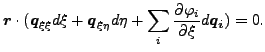 |
(79) |
最終的に以下の式が得られます。
![$\displaystyle - \boldsymbol{q}_{\xi} \cdot d \boldsymbol{p} + \sum_i \left[ (\...
...tial \varphi_i}{\partial \xi } \boldsymbol{r}) \cdot d \boldsymbol{q_i} \right]$](img565.png) |
(80) |
η-方向の接線についても同様です。
![$\displaystyle - \boldsymbol{q}_{\eta} \cdot d \boldsymbol{p} + \sum_i \left[ (...
...ial \varphi_i}{\partial \eta } \boldsymbol{r}) \cdot d \boldsymbol{q_i} \right]$](img567.png) |
(81) |
これから、![]() 、
、![]() などが求まります。dqi, i=1,..,nm = 0 、dpy = dpz = 0 と仮定しましょう。すると上式の右辺は -qξxdpx、-qηxdpx となり、最終的に2つの未知数
などが求まります。dqi, i=1,..,nm = 0 、dpy = dpz = 0 と仮定しましょう。すると上式の右辺は -qξxdpx、-qηxdpx となり、最終的に2つの未知数![]() 、
、![]() を持つ2つの方程式になります。
を持つ2つの方程式になります。![]() が決まれば以下の式から自動的に
が決まれば以下の式から自動的に![]() が決定します。
が決定します。
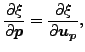 |
(82) |
他の導関数についても同様です。これによって導関数![]() が決定されます。
が決定されます。
以下の式
| (83) |
から、次が得られます。
これがマスター節点での力の導関数になります。