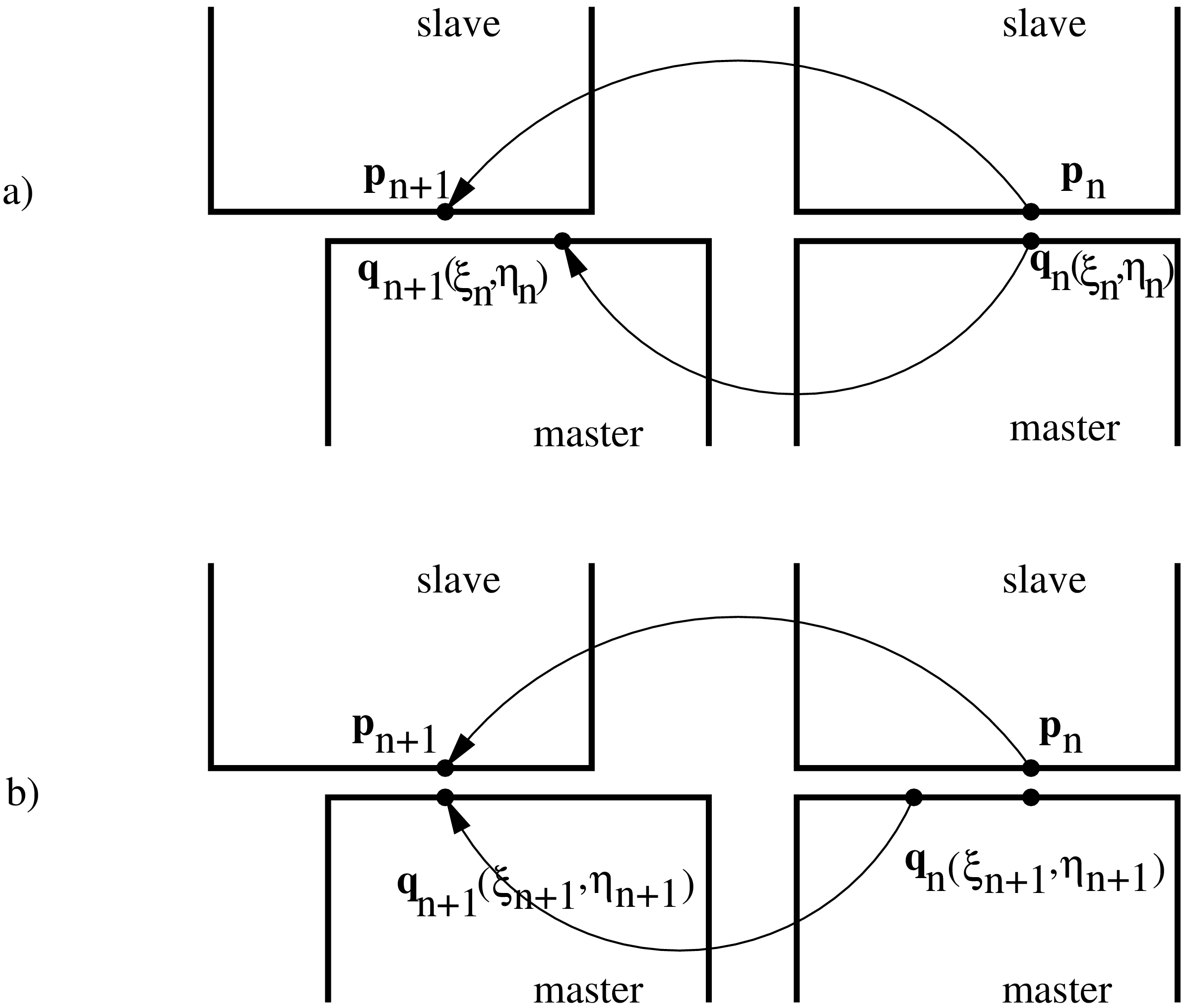
接線方向の接触剛性

次へ上へ前へ目次へ
次へ：Face-to-Face Penalty Contact 上へ：Node-to-Face Penalty Contact 前へ：Normal contact stiffness 目次へ

接線方向の接触剛性

**図114:** 接線方向の差分変位を可視化したもの
$\begin{figure}\epsfig{file=tangentcontact.eps,width=12cm}\end{figure}$

接線方向の接触剛性行列を求めるためには、まず図114の a) を見てください。時刻 t_n で特徴づけられるある時間増分の開始時、スレーブ節点の位置を p_n とし、それと対応するマスター側の投影ベクトルを q_n とします。時刻 t_n+1 で特徴づけられる時間増分の終了時、両者はそれぞれ位置 p_n+1 と q_n+1 へ移動します。この増分の間に差分変位は以下の式を満たすベクトル s によって変化します。

s = (p_n+1 - q_n+1) - (p_n - q_n)

(85)

ここで q_n は以下を満たします。

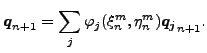$\displaystyle \boldsymbol{q}_{n+1}= \sum_j \varphi_j(\xi^m _n, \eta^m_n) \boldsymbol{q_j}_{n+1} .$

(86)

ローカル座標は時刻 t_n での値であることに注意してください。接線方向変位の差分は以下の様に変形されます。

t = s - n

(87)

ここで s は以下の通りです。

s = s・n

(88)

u_i に対する導関数は以下を満足します（簡単な微分）。

$\displaystyle \frac{\partial \boldsymbol{t} }{\partial \boldsymbol{u_i} } = \fr... ...ldsymbol{u_i} } - s \frac{\partial \boldsymbol{n} }{\partial \boldsymbol{u_i} }$

(89)

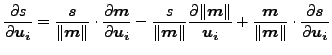$\displaystyle \frac{\partial s}{\partial \boldsymbol{u_i} } = \frac{\boldsymbol... ...bol{m}\Vert } \cdot \frac{\partial \boldsymbol{s} }{\partial \boldsymbol{u_i} }$

(90)

また以下の通りです。

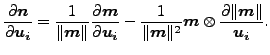$\displaystyle \frac{\partial \boldsymbol{n} }{\partial \boldsymbol{u_i} } = \fr... ...bol{m } \otimes \frac{\partial \Vert \boldsymbol{m} \Vert }{\boldsymbol{u_i} }.$

(91)

ξ と η を固定することで r の u_i に対する導関数から s の u_i に対する導関数が求められます（この導関数は t_n+1 でのものであることに注意してください。結果、t_n での値の導関数は全て消えます）。

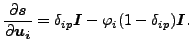$\displaystyle \frac{\partial \boldsymbol{s} }{\partial \boldsymbol{u_i} } = \delta _{ip} \boldsymbol{I} - \varphi_i (1 - \delta _{ip}) \boldsymbol{I}.$

(92)

物理的には接線方向接触の方程式は以下の様になります（スレーブ節点 p の位置での記述）。

接着 t³ 、スリップ t^p での接線方向の差分変位の加法型分解

t = t^e + t^p (93)
スレーブ節点 p の位置でスレーブ側からマスター側へ働く接線方向の力を定義する接着則（ $K_t\equiv \lambda a_p$ 。ここで λ は接着勾配、a_p は接着しているスレーブ節点の代表スレーブ面積）

F_T = K_tt^e (94)
クーロン・スリップ限界

$\displaystyle \Vert \boldsymbol{F_T} \Vert \le \mu \Vert \boldsymbol{F_N} \Vert$ (95)
スリップの発展方程式

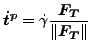$\displaystyle \boldsymbol{\boldsymbol{\dot{t}^p} }= \dot{\gamma} \frac{\boldsymbol{F_T} }{\Vert \boldsymbol{F_T} \Vert }$ (96)

まず、接線方向の差分変位の加法型分解の異なる式形を導きます。以下の式から開始します。

t = t^e + t^p

(97)

時間微分をとることで以下が得られます。

$\displaystyle \boldsymbol{\dot{t}}= \boldsymbol{\dot{t}^e} + \boldsymbol{\dot{t}^p}.$

(98)

スリップの発展方程式を代入すると以下の様になります。

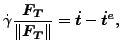$\displaystyle \dot{\gamma} \frac{\boldsymbol{F_T} }{\Vert \boldsymbol{F_T} \Vert }=\boldsymbol{\dot{t}} - \boldsymbol{\dot{t}^e},$

(99)

さらに K_t をかけると次の様になります。

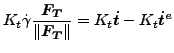$\displaystyle K_t \dot{\gamma} \frac{\boldsymbol{F_T} }{\Vert \boldsymbol{F_T} \Vert }=K_t \boldsymbol{\dot{t}} - K_t \boldsymbol{\dot{t}^e}$

(100)

有限差分（後退オイラー）を使用してこの式を t_n+1 で書くと次の式が得られます。

$\displaystyle K_t \Delta \gamma_{n+1} \frac{\boldsymbol{F_T}_{n+1} }{\Vert\bold... ...lta \boldsymbol{t}_{n+1} - K_t \boldsymbol{t^e}_{n+1} + K_t \boldsymbol{t^e}_n,$

(101)

ここで $\Delta \gamma_{n+1} \equiv \dot{\gamma} _{n+1} \Delta t$ 、 $\Delta \boldsymbol{t}_{n+1} \equiv \boldsymbol{t}_{n+1} - \boldsymbol{t}_n$ です。パラメーター K_t は時間非依存と考えられます。

ここで支配方程式を解くためにラジアルリターンアルゴリズムを書き下しておきましょう。時刻 t_n での解が既知である、つまり t^e_n と t^p_n がわかっているとしましょう。接着則を使うと F_{T_n} を計算することができます。今。私たちが知りたいのは時刻 t_n+1 でのこれら変数なので、全微分された接線方向変位 t_n+1 を考えます。まず予備的な接線方向の力 $\boldsymbol{F_T}_{n+1}^{trial}$ を考えます。この力は時刻 t_n+1 における力で t_n から t_n+1 までの間にスリップは起きていないものとします。この仮定は t^p_n+1=t^p_n と等価です。従って予備的な接線方向の力は以下を満たします（接着則を参照）

$\displaystyle \boldsymbol{F_T}_{n+1}^{trial} = K_t(\boldsymbol{t}_{n+1} - \boldsymbol{t^p}_n).$

(102)

この式は以下の様に書くこともできます。

$\displaystyle \boldsymbol{F_T}_{n+1}^{trial} = K_t(\boldsymbol{t}_{n+1} - \boldsymbol{t}_n + \boldsymbol{t}_n - \boldsymbol{t^p}_n).$

(103)

さらに次の様にできます。

$\displaystyle \boldsymbol{F_T}_{n+1}^{trial} = K_t \Delta \boldsymbol{t}_{n+1} + K_t \boldsymbol{t^e}_n.$

(104)

式（101）を使うと、これは以下と等しくなります。

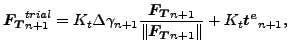$\displaystyle \boldsymbol{F_T}_{n+1}^{trial} = K_t \Delta \gamma_{n+1} \frac{\b... ...l{F_T}_{n+1} }{\Vert\boldsymbol{F_T}_{n+1} \Vert} + K_t \boldsymbol{t^e}_{n+1},$

(105)

さらに次の様にできます。

$\displaystyle \boldsymbol{F_T}_{n+1}^{trial} = (K_t \Delta \gamma_{n+1} \frac{1 }{\Vert\boldsymbol{F_T}_{n+1} \Vert} + 1) \boldsymbol{F_T}_{n+1} .$

(106)

最後の式から次が得られます。

$\displaystyle \boldsymbol{F_T}_{n+1}^{trial} \parallel \boldsymbol{F_T}_{n+1}$

(107)

また式（106）のかっこ内の項は両方、正の値なので次の様になります。

$\displaystyle \Vert \boldsymbol{F_T}_{n+1}^{trial}\Vert = K_t \Delta \gamma_{n+1} + \Vert \boldsymbol{F_T}_{n+1} \Vert.$

(108)

満足するべき式で残されたのはクーロン・スリップ限界だけです。ここでは2つの可能性があります。

$\Vert \boldsymbol{F_T}_{n+1}^{trial}\Vert \le \mu \Vert \boldsymbol{F_N}_{n+1} \Vert$ .
この場合、クーロン・スリップ限界が満たされ、以下の解が求まります。

$\displaystyle \boldsymbol{F_T}_{n+1} = \boldsymbol{F_T}_{n+1}^{trial} = K_t(\boldsymbol{t_{n+1}} - \boldsymbol{t^p}_n)$ (109)

また以下の様になります。

$\displaystyle \frac{\partial \boldsymbol{F_T}_{n+1}}{\partial \boldsymbol{t}_{n+1} } = K_t \boldsymbol{I}.$ (110)

t_n から t_n+1 の間でさらにスリップが起きることはありません。
$\Vert \boldsymbol{F_T}_{n+1}^{trial}\Vert > \mu \Vert \boldsymbol{F_N}_{n+1} \Vert$ .
この場合には解をスリップ面に逆写像し、また $\Vert \boldsymbol{F_T}_{n+1}\Vert = \mu \Vert \boldsymbol{F_N}_{n+1} \Vert$ であることが必要です。式（108）を使うと堅さのパラメーター γ の増加に対する以下の式が導かれます。

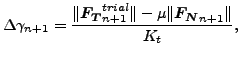$\displaystyle \Delta \gamma _{n+1}= \frac{\Vert\boldsymbol{F_T}_{n+1}^{trial}\Vert- \mu \Vert \boldsymbol{F_N}_{n+1} \Vert }{K_t},$ (111)

これを使用して t^p を更新することができます（スリップ発展方程式を使用）。

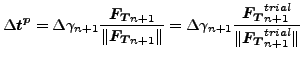$\displaystyle \Delta \boldsymbol{t^p}= \Delta \gamma_{n+1} \frac{\boldsymbol{F_... ...rac{\boldsymbol{F_T}_{n+1}^{trial} }{\Vert\boldsymbol{F_T}_{n+1}^{trial} \Vert}$ (112)

接線方向の力は以下の様に書けます。

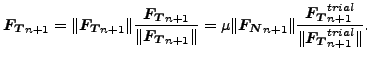$\displaystyle \boldsymbol{F_T}_{n+1}= \Vert \boldsymbol{F_T}_{n+1} \Vert \frac{... ...c{\boldsymbol{F_T}_{n+1}^{trial}}{\Vert \boldsymbol{F_T}_{n+1}^{trial} \Vert }.$ (113)

さて

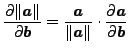$\displaystyle \frac{\partial \Vert \boldsymbol{a} \Vert}{\partial \boldsymbol{b... ...ymbol{a}\Vert } \cdot \frac{\partial \boldsymbol{a} }{\partial \boldsymbol{b} }$ (114)

であり

$\displaystyle \frac{\partial }{\partial \boldsymbol{b} } \left (\frac{\boldsymb... ...ght) \right ] \cdot \frac{\partial \boldsymbol{a} }{\partial \boldsymbol{b} },$ (115)

です。ここで a と b はベクトルです。これによって以下の接線方向の力の導関数を得られます。

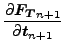$\displaystyle \frac{\partial \boldsymbol{F_T}_{n+1} }{\partial \boldsymbol{t}_{n+1} }$ $\displaystyle = \mu \boldsymbol{\xi }_{n+1} \otimes \left [ \frac{\boldsymbol{F... ...t \frac{\partial \boldsymbol{F_N}_{n+1}}{\partial \boldsymbol{t}_{n+1}} \right]$

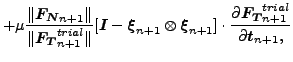$\displaystyle + \mu \frac{\Vert\boldsymbol{F_N}_{n+1} \Vert}{\Vert\boldsymbol{F... ...frac{\partial \boldsymbol{F_T}_{n+1}^{trial} }{\partial \boldsymbol{t}_{n+1}, }$ (116)

ここで

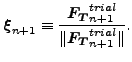$\displaystyle \boldsymbol{\xi }_{n+1} \equiv \frac{\boldsymbol{F_T}_{n+1}^{trial}}{\Vert \boldsymbol{F_T}_{n+1}^{trial} \Vert }.$ (117)

です。最終的に（式110を使用して）以下が得られます。

$\displaystyle \frac{\partial \boldsymbol{F_T}_{n+1} }{\partial \boldsymbol{u_i}_{n+1} }$ $\displaystyle = \mu \boldsymbol{\xi }_{n+1} \otimes \left [ -\boldsymbol{n} \cdot \frac{\partial \boldsymbol{F_N}_{n+1}}{\partial \boldsymbol{u_i}_{n+1}} \right]$

$\displaystyle + \mu \frac{\Vert\boldsymbol{F_N}_{n+1} \Vert}{\Vert\boldsymbol{F... ...ot K_t \frac{\partial \boldsymbol{t}_{n+1} }{\partial \boldsymbol{u_i}_{n+1}. }$ (118)

右辺の量はすべて既にわかっています（式（70）と式（89）を参照）。
CalculiXの節点・面接触では式（85）が変形され簡略化されています。q_n+1 が p_n+1 と q_n の写像だとすると以下の様に変形されています（図114の b) を参照）。

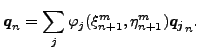$\displaystyle \boldsymbol{q}_{n}= \sum_j \varphi_j(\xi^m _{n+1}, \eta^m_{n+1}) \boldsymbol{q_j}_{n} .$ (119)

図の a) と b) は実質的に同じ、同じものを別の視点で表しているだけです。a) ではマスター面への投影は時刻 t_n で行なわれ、差分変位は時刻 t_n+1 で計算されます。b) では投影は時刻 t_n+1 で行なわれ、差分変位は時刻 t_n で計算されます。さて実際の位置は変形前の位置と変形の和として書き表せます。従って p=(X+v)^s、q=(X+v)^m から以下の様になります。

$\displaystyle \boldsymbol{s}=(\boldsymbol{X}+\boldsymbol{v})^s_{n+1} - (\boldsy... ...mbol{v})^s_n + (\boldsymbol{X}+\boldsymbol{v})^m_n(\xi^m _{n+1}, \eta^m_{n+1}).$ (120)

変形前の位置は時間に依存しないので以下の様に消すことができます。

$\displaystyle \boldsymbol{s}=\boldsymbol{v}^s_{n+1} - \boldsymbol{v}^m_{n+1}(\x... ...a^m_{n+1}) -\boldsymbol{v}^s_n + \boldsymbol{v}^m_n(\xi^m _{n+1}, \eta^m_{n+1})$ (121)

さらに次の様になります。

$\displaystyle \boldsymbol{s}$ $\displaystyle =\boldsymbol{v}^s_{n+1} - \boldsymbol{v}^m_{n+1}(\xi^m _{n+1}, \e... ...n+1}) -\boldsymbol{v}^s_n + \boldsymbol{v}^m_n(\xi^m _{n}, \eta^m_{n})\noindent$ (122)

$\displaystyle + \boldsymbol{v}^m_n(\xi^m _{n+1}, \eta^m_{n+1})- \boldsymbol{v}^m_n(\xi^m _{n}, \eta^m_{n})$ (123)

さらに最後の2つの項も消します。つまり時刻 t_n での位置 $(\xi^m _{n}, \eta^m_{n})$ と $(\xi^m _{n+1}, \eta^m_{n+1})$ の間の変形の差分は t_n から t_n+1 の間の移動の差分と比べて無視可能であると見なすのです。すると s の式は以下の様に簡略化できます。

$\displaystyle \boldsymbol{s}=\boldsymbol{v}^s_{n+1} - \boldsymbol{v}^m_{n+1}(\x... ...\eta^m_{n+1}) -\boldsymbol{v}^s_n + \boldsymbol{v}^m_n(\xi^m _{n}, \eta^m_{n}),$ (124)

以上から保持すべき量は実際の時刻とインクリメント開始時の時刻での p と q の間の変形の差分であることがわかります。

次へ上へ前へ目次へ
次へ：Face-to-Face Penalty Contact 上へ：Node-to-Face Penalty Contact 前へ：Normal contact stiffness 目次へ

guido dhondt 2016-03-08

$\displaystyle \frac{\partial \boldsymbol{F_T}_{n+1} }{\partial \boldsymbol{t}_{n+1} }$	$\displaystyle = \mu \boldsymbol{\xi }_{n+1} \otimes \left [ \frac{\boldsymbol{F... ...t \frac{\partial \boldsymbol{F_N}_{n+1}}{\partial \boldsymbol{t}_{n+1}} \right]$
	$\displaystyle + \mu \frac{\Vert\boldsymbol{F_N}_{n+1} \Vert}{\Vert\boldsymbol{F... ...frac{\partial \boldsymbol{F_T}_{n+1}^{trial} }{\partial \boldsymbol{t}_{n+1}, }$	(116)

$\displaystyle \boldsymbol{s}$	$\displaystyle =\boldsymbol{v}^s_{n+1} - \boldsymbol{v}^m_{n+1}(\xi^m _{n+1}, \e... ...n+1}) -\boldsymbol{v}^s_n + \boldsymbol{v}^m_n(\xi^m _{n}, \eta^m_{n})\noindent$	(122)
	$\displaystyle + \boldsymbol{v}^m_n(\xi^m _{n+1}, \eta^m_{n+1})- \boldsymbol{v}^m_n(\xi^m _{n}, \eta^m_{n})$	(123)