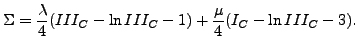大ひずみのための線形弾性材料（Ciarletのモデル）

[18]では古典的なフックの法則における微小変形をラグランジュひずみと第2 Piola-Kirchhoff 応力による応力で置き換えても物理的に理解可能な材料法則は導かれないと説明されています。実際、そのようなモデル（St-Venant-Kirchoff 材料とも呼ばれます）はゼロ付近まで材料体積を圧縮しても大きな応力を示すことはありません。このモデルに代わるのが Ciarlet によって作り出された次に示す蓄積エネルギー関数です [17]。

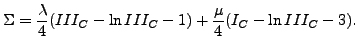$\displaystyle \Sigma = \frac{\lambda}{4}(III_C - \ln III_C -1) + \frac{\mu }{4}(I_C - \ln III_C -3).$

(147)

応力とひずみの関係は以下の様になります（S は第2 Piola-Kirchhoff 応力）。

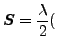$\displaystyle \boldsymbol{S}= \frac{\lambda}{2}($ det $\displaystyle \boldsymbol{C} -1) \boldsymbol{C^{-1}} + \mu (\boldsymbol{I}-\boldsymbol{C^{-1}}) ,$

(148)

S をGreenテンソル E で微分すると以下のようなります（成分表記）。

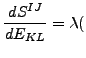$\displaystyle \frac{d S^{IJ} }{d E_{KL} } = \lambda ($ det $\displaystyle \boldsymbol{C}) C^{{-1}^{KL}} C^{{-1}^{IJ}}+[2 \mu - \lambda ($ det $\displaystyle \boldsymbol{C} -1)] C^{{-1}^{IK}} C^{{-1}^{LJ}}.$

(149)

このモデルを CalculiX に実装したのは Sven Kaßbohm です。定義は材料の名前を定義する *MATERIAL カードから構成されます。材料名は上限は80文字で必ず「CIARLET_EL」から始まらなければなりませんが、残りの70文字は自由に設定することができます。材料定義内では *USER MATERIAL カードは以下の様に使用しなければなりません。

全ての温度依存性を定義する必要がある場合にはこの行を繰り返します。

温度400で λ =121153.85、μ =80769.23 の弾性定数を持つ単結晶をを定義しています。

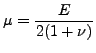$\displaystyle \mu= \frac{E}{2(1+\nu)}$

(150)

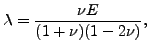$\displaystyle \lambda=\frac{\nu E}{(1+\nu)(1-2 \nu)},$

(151)

であることを思い出してください。ここで E はヤング率、ν はポアソン係数です。