定常地下水流れ

定常地下水流れの支配方程式は以下の通りです（Darcy の法則とも呼ばれます）[27]

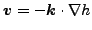$\displaystyle \boldsymbol{ v} = - \boldsymbol{k} \cdot \nabla h$

(220)

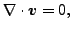$\displaystyle \nabla \cdot \boldsymbol{ v} = 0,$

(221)

ここで v は排出流速、k は浸透テンソル、h は以下で定義される総水頭です。

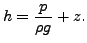$\displaystyle h = \frac{p}{\rho g} + z.$

(222)

後の式の p は地下水圧力、ρ はその密度、z は参照位置から見た高さです。排出流速は単位時間あたりに多孔質体の単位総面積を通過する流体量を指します。

これら方程式の結果から以下の様になります。

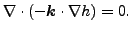$\displaystyle \nabla \cdot (- \boldsymbol{ k} \cdot \nabla h) = 0.$

(223)

熱方程式と比較すると、その対応関係は表（15）の様になります。地下水流れ方程式は定常状態方程式で、熱容量に相当する項を持たないことに注意してください。

可能な境界条件は以下の通りです。

水面下の非浸透性面。水面を基準位置にとり、空気の圧力を p₀ とすると総水頭は以下の様になります。

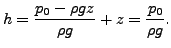$\displaystyle h = \frac{p_0 - \rho g z}{\rho g} + z = \frac{p_0}{\rho g}.$ (224)
浸透面、つまり地面と空気の間の境界。以下の様になります。

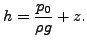$\displaystyle h = \frac{p_0}{\rho g} + z.$ (225)
非浸透性面： v_n=0
自由面、つまり地面下の地下水流れの上側境界。ここでは2つの条件が満たされなければなりません。まず自由面に沿って以下の様にならなければなりません。

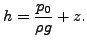$\displaystyle h = \frac{p_0}{\rho g} + z.$ (226)

また自由面に垂直な n 方向では v_n=0 とならなければなりません。ただし問題においては自由面の正確な位置は未知数です。これは両方の式が満足されるまで繰り返し計算を行なうことで決定されます。

guido dhondt 2016-03-08