次へ 上へ 前へ 目次へ
次へ：*HYPERFOAM 上へ：Input deck format 前へ：*HEAT TRANSFER 目次へ


*HYPERELASTIC

キーワードのタイプ：モデル定義、材料

このオプションを使用すると材料の超弾性プロパティーを定義できます。オプションパラメーターは2つあります。1つ目はモデルを定義するもので、ARRUDA-BOYCE、MOONEY-RIVLIN、NEO HOOKE、OGDEN、POLYNOMIAL、REDUCED POLYNOMIAL、YEOH の文字列のうちのどれかを取ります。2つ目のパラメーター N は OGDEN モデル、POLYNOMIAL モデル、REDUCED POLYMIAL モデルのみで意味を持つもので、ひずみエネルギーポテンシャルの次数を決めます。デフォルトは N=1 の POLYNOMIAL モデルです。定数は全て温度依存可能です。

さて$ \bar{I}_1$、$ \bar{I}_2$、J を以下で定義したとしましょう。

$ \bar{I}_1$ = $\displaystyle III_C^{-1/3} I_C$ (342)
$ \bar{I}_2$ = $\displaystyle III_C^{-1/3} II_C$ (343)
$\displaystyle J$ = $\displaystyle III_C^{1/2}$ (344)

ここで IC 、IIC、IIIC は右 Cauchy-Green 変形テンソルの不変量 CKL = xk,Kxk,L です。テンソル CKL はラグランジュひずみテンソル EKL と以下によって結びついています。
2EKL = CKL - δKL (345)

ここで δ はクロネッカー記号です。file:///D:/Workspace/Calculix/Doc-Temp/ccx-2.10-temp/img1374.png

Arruda-Boyce ひずみエネルギーポテンシャルは以下の形を取ります。

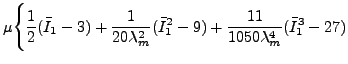$\displaystyle U$ $\displaystyle =$ $\displaystyle \mu \Bigg\{ \frac{1}{2}(\bar{I}_1-3)+\frac{1}{20\lambda_m^2}(\bar{I}_1^2-9)+\frac{11}{1050\lambda_m^4}(\bar{I}_1^3-27)$
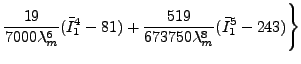+ $\displaystyle \frac{19}{7000\lambda_m^6}(\bar{I}_1^4-81)+\frac{519}{673750\lambda_m^8}(\bar{I}_1^5-243) \Bigg\}$ (346)
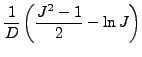+ $\displaystyle \frac{1}{D} \left(\frac{J^2-1}{2} - \ln J \right)$

また Mooney-Rivlin ひずみエネルギーポテンシャルは以下の形を取ります。

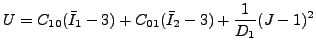$\displaystyle U=C_{10}(\bar{I}_1-3)+C_{01}(\bar{I}_2-3)+\frac{1}{D_1}(J-1)^2$ (347)

Mooney-Rivlin ひずみエネルギーポテンシャルは N=1 での多項式ひずみエネルギーポテンシャルと一致します。

Neo-Hooke ひずみエネルギーポテンシャルは以下の形を取ります。

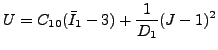$\displaystyle U=C_{10}(\bar{I}_1-3)+\frac{1}{D_1}(J-1)^2$ (348)

Neo-Hooke ひずみエネルギーポテンシャルは N=1 での低減された多項式エネルギーポテンシャルと一致します。

多項式ひずみエネルギーポテンシャルは以下の形を取ります。

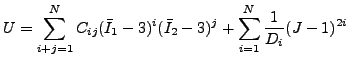$\displaystyle U=\sum_{i+j=1}^{N} C_{ij}(\bar{I}_1-3)^i(\bar{I}_2-3)^j +\sum_{i=1}^{N}\frac{1}{D_i}(J-1)^{2i}$ (349)

CalculiX では N≤3です。

低減された多項式ひずみエネルギーポテンシャルは以下の形を取ります。

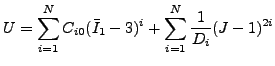$\displaystyle U=\sum_{i=1}^{N} C_{i0}(\bar{I}_1-3)^i +\sum_{i=1}^{N}\frac{1}{D_i}(J-1)^{2i}$ (350)

CalculiX では N≤3です。低減された多項式ひずみエネルギーポテンシャルは多項式ひずみエネルギーポテンシャルの特殊な場合と見ることができます。

Yeoh のひずみエネルギーポテンシャルは N＝3 での低減された多項式ひずみエネルギーポテンシャルに他なりません。

主ストレッチをλ1、λ2、λ3（$ \lambda_1^2$、$ \lambda_2^2$、$ \lambda_3^2$を右 Cauchy-Green 変形テンソルの固有値とします）で記述し、また$ \bar{\lambda}_i=III_C^{-1/6}\lambda_i$として偏差ひずみを$ \bar{\lambda}_1$、$ \bar{\lambda}_2$、$ \bar{\lambda}_3$で記述すると、Ogden のひずみエネルギーポテンシャルは以下の形を取ります。

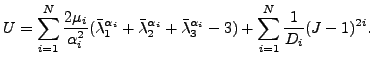$\displaystyle U=\sum_{i=1}^{N} \frac{2 \mu_i}{\alpha_i^2}(\bar{\lambda}_1^{\alp... ...{\alpha_i}+\bar{\lambda}_3^{\alpha_i}-3)+\sum_{i=1}^{N}\frac{1}{D_i}(J-1)^{2i}.$ (351)

超弾性材料の入力デッキは以下の様になります。


1行目：

ARRUDA-BOYCE モデルの場合は以下の行

完全な温度依存性を定義する必要がある場合はこの行を繰り返してください。

MOONEY-RIVLIN モデルの場合は以下の行

完全な温度依存性を定義する必要がある場合はこの行を繰り返してください。

NEO-HOOKE モデルの場合は以下の行

完全な温度依存性を定義する必要がある場合はこの行を繰り返してください。

N=1 の OGDEN モデルの場合は以下の行

完全な温度依存性を定義する必要がある場合はこの行を繰り返してください。

N=2 の OGDEN モデルの場合は以下の行

完全な温度依存性を定義する必要がある場合はこの行を繰り返してください。

N=3 の OGDEN モデルの場合は以下のペアの行
ペアの1行目

ペアの2行目 完全な温度依存性を定義する必要がある場合はこのペアを繰り返してください。 -->

N=1 の POLYNOMIAL モデルの場合は以下の行

完全な温度依存性を定義する必要がある場合はこの行を繰り返してください。

N=2 の POLYNOMIAL モデルの場合は以下の行

完全な温度依存性を定義する必要がある場合はこの行を繰り返してください。

N=3 の POLYNOMIAL モデルの場合は以下のペアの行
ペアの1行目

ペアの2行目 完全な温度依存性を定義する必要がある場合はこのペアを繰り返してください。

N=1 の REDUCED POLYNOMIAL モデルの場合は以下の行

完全な温度依存性を定義する必要がある場合はこの行を繰り返してください。

N=2 の REDUCED POLYNOMIAL モデルの場合は以下の行

完全な温度依存性を定義する必要がある場合はこの行を繰り返してください。

N=3 の REDUCED POLYNOMIAL モデルの場合は以下の行

完全な温度依存性を定義する必要がある場合はこの行を繰り返してください。

YEOH モデルの場合は以下の行

完全な温度依存性を定義する必要がある場合はこの行を繰り返してください。 

例：
*HYPERELASTIC,OGDEN,N=1
3.488,2.163,0.

上記では、μ1 = 3.488、α1 = 2.163、D1 =0の、項が1つの Ogden 材料を定義しています。圧縮性係数にゼロを設定しているので、一定の圧縮性によって収束性を保証するためにこの値は CalculiX によって小さな値に置き換えられます（ページ[*]を参照）。


サンプルファイル: beamnh、beamog

次へ 上へ 前へ 目次へ
次へ：*HYPERFOAM 上へ：Input deck format 前へ：*HEAT TRANSFER 目次へ
guido dhondt 2016-03-08