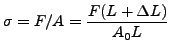 |
(155) |
変形塑性はへずみと応力の1対1(全単射)の関係で特徴づけられます。この関係は1次元の Ramberg-Osgood 則の3次元への一般化と言えます。これはひずみ関数に対して 応力関数が単調増加的に従う(例えば簡単な引張試験などでの)金属材料でよく使用されます。従って変形塑性は Cauchy(真)応力とひずみの間の関係のモデル化に非常に向いています。Cauchy 応力と対数ひずみ(以下ですぐに定義します)の関係をプロットすると張力や圧力のテスト結果がよく合うため、これらの量は変形塑性則で一般的に使われます。しかし CalculiX の実装(*DEFORMATION PLASTICITY キーワード・カード)ではCauchy(真)応力のオイラーひずみに対する依存をモデル化した関係を使用しています。実際的な目的においてはオイラーひずみは対数ひずみと一致します。引張試験試料を考え、初期長さ L、初期断面積 A0、最終長さ A、荷重 F、Cauchy 応力 σ 、対数ひずみ εlog 、オイラーひずみ εEuler とすると以下の式が満たされます。
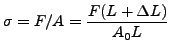 |
(155) |
![$\displaystyle \epsilon_{log}=ln \left[1+\frac{\Delta L}{L} \right]$](img738.png) |
(156) |
![$\displaystyle \epsilon_{Euler}=\frac{\Delta L}{L}\left[1-\frac{\Delta L}{2L} \right]$](img739.png) |
(157) |
対数ひずみとオイラーひずみの差は工学ひずみ ΔL/L = 20% に対して1.3 %です。ユーザーは Ramberg-Osgood 材料定数を(Cauchy 応力とオイラーひずみの関係をプロットし、フィッテイングを行なうことで)直接、設定する必要があります。