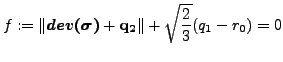次へ 上へ 前へ 目次へ
次へ：Elastic anisotropy with isotropic 上へ：Materials 前へ：The Cailletaud single crystal 目次へ

等方的な粘塑性をもつ弾性異方性

フォン・ミーゼス型の降伏曲面を持つ弾性異方性材料の微小変形を記述するためのモデルです。このモデルは、粘塑性領域での異方的挙動のデータがなかったり、性質がよくわからない異方性材料の暫定的な代替としてよく使用されます。

全ひずみは弾性ひずみと塑性ひずみの和と仮定されます。

ε = εe + εp (175)

降伏曲面の等方変化、移動変化を荒らすために等方硬化変数 q1 と移動硬化テンソル q2 がそれぞれ導入されています。降伏曲面は以下のように書けます。

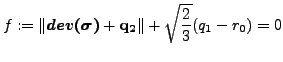$\displaystyle f := \left\Vert \mbox{\boldmath {$dev({\sigma})$}} + \mathbf{q_2} \right\Vert + \sqrt{\frac{2}{3}}(q_1-r_0) = 0$ (176)

ここで dev(σ) は偏差応力テンソル、r0 はゼロ降伏での弾性範囲のサイズです。硬化変数の構成方程式は以下を満たします。

q1 = -d1α1 (177)

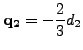$\displaystyle \mathbf{q_2} = - \frac{2}{3} d_2$$\displaystyle \mbox{\boldmath${\alpha_2}$}$ (178)

ここで α1 と α2 はひずみ空間内の硬化変数です。これは以下の様に書くことができます。

α1 = εpeq (179)

α2eq = εpeq (180)

ここで εpeq は以下で定義される等価塑性ひずみです。

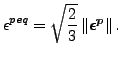$\displaystyle {\epsilon}^{peq} = \sqrt{\frac{2}{3}} \left \Vert \mbox{\boldmath${{\epsilon}^p}$} \right \Vert.$ (181)

また α2eq は同様に定義されるテンソル α2 の等価値です。以上から構成方程式は以下の様になります。

q1 = -d1εpeq (182)

q2eq = d2εpeq
(183)

ここで

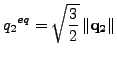$\displaystyle {q_2}^{eq} = \sqrt{\frac{3}{2}} \left \Vert \mathbf{q_2} \right \Vert$ (184)

は等価応力値、またはフォン・ミーゼス値を意味します。同じことが q1 にも当てはまります。結果、構成方程式は硬化応力と等価塑性ひずみの間の線形関係となります。

応力の構成方程式はフック則です。

σ = C : εe (185)

塑性ひずみの発展方程式とひずみ空間での硬化変数は以下で与えられます。

$\displaystyle \mbox{\boldmath${\dot{\epsilon}^p}$}$$\displaystyle = \dot{\gamma} \mathbf{n},$ (186)

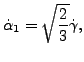$\displaystyle \dot{\alpha}_1 = \sqrt{\frac{2}{3}} \dot{\gamma},$ (187)

$\displaystyle \mbox{\boldmath${\dot{\alpha}_2}$}$$\displaystyle = \dot{\gamma} \mathbf{n},$ (188)

ここで

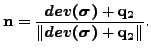$\displaystyle \mathbf{n} = \frac {\mbox{\boldmath${dev(\sigma)}$} + \mathbf{q_2}} {\left \Vert \mbox{\boldmath${dev(\sigma)}$} + \mathbf{q_2} \right \Vert }.$ (189)

変数$ \dot{\gamma}$は最適化理論での Kuhn-Tucker 条件から求められた硬さ係数[44]です。これは以下を満たします。

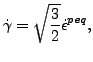$\displaystyle \dot{\gamma} = \sqrt{\frac{3}{2}} \dot{\epsilon}^{peq},$ (190)

最後に、クリープ速度は降伏超過と総時間 t のべき関数としてモデル化されます。

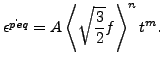$\displaystyle \dot{\epsilon^{peq}} = A \left \langle \sqrt{\frac{3}{2}} f \right \rangle ^ {n} t^m.$ (191)

ブラケット$ \langle \rangle$は負の値をゼロに、正の値をそのままにすることを意味します。つまり x < 0 では 〈x〉 = 0 、x ≥ 0 では 〈x〉 = x となります。

現在の実装では直交異方性の弾性挙動が仮定されています。その結果、各温度ごとに15の定数を定義する必要があります。弾性定数 C1111 、C1122 、C2222 、C1133 、C2233 、C3333 、C1212 、C1313 、C2323 と粘塑性定数 r0、d1、d2、A、n、m です。

材料定義は、材料名を定義する *MATERIAL から構成されます。この名前は必ず「ANISO_PLAS」から始まり、80文字以内でなければなりません。残りの70文字に関しては自由に設定することができます。材料定義内では *USER MATERIAL カードは以下を満たす必要があります。

1行目：

以降の行は2つのセットからなります：


セットの1行目：

セットの2行目：

完全な温度依存性を定義する必要がある場合はこのセットを繰り返してください。

材料の第1軸はグローバル座標系と一致するとみなされます。もしそうでない場合には *ORIENTATION カードを使用してローカル座標系を定義してください。

このモデルでは14の内部状態変数があります。

これらの変数は *EL PRINT キーワード（.datファイル）と *EL FILE キーワード（.frdファイル）で順番に従ってアクセスすることができます（SDVラベル）。また*DEPVAR カードを材料定義内で値14とともに設定する必要があります。 

例:
*MATERIAL,NAME=ANISO_PLAS
*USER MATERIAL,CONSTANTS=15
500000.,157200.,500000.,157200.,157200.,500000.,126200.,126200.,
126200.,0.,0.,0.,1.E-10,5,0.
*DEPVAR
14

弾性定数500000.、157200.、500000.、157200.、157200.、500000.、126200.、126200.、126200.、粘塑性パラメーター r0=0.、d1=0.、d2=0.、A=10-10、n=5、m=0 の単結晶を定義。定義から降伏曲面がゼロ半径を持ち、硬化はありません。クリープだけが有効化されています。

次へ 上へ 前へ 目次へ
次へ：Elastic anisotropy with isotropic 上へ：Materials 前へ：The Cailletaud single crystal 目次へ
guido dhondt 2016-03-08