 |
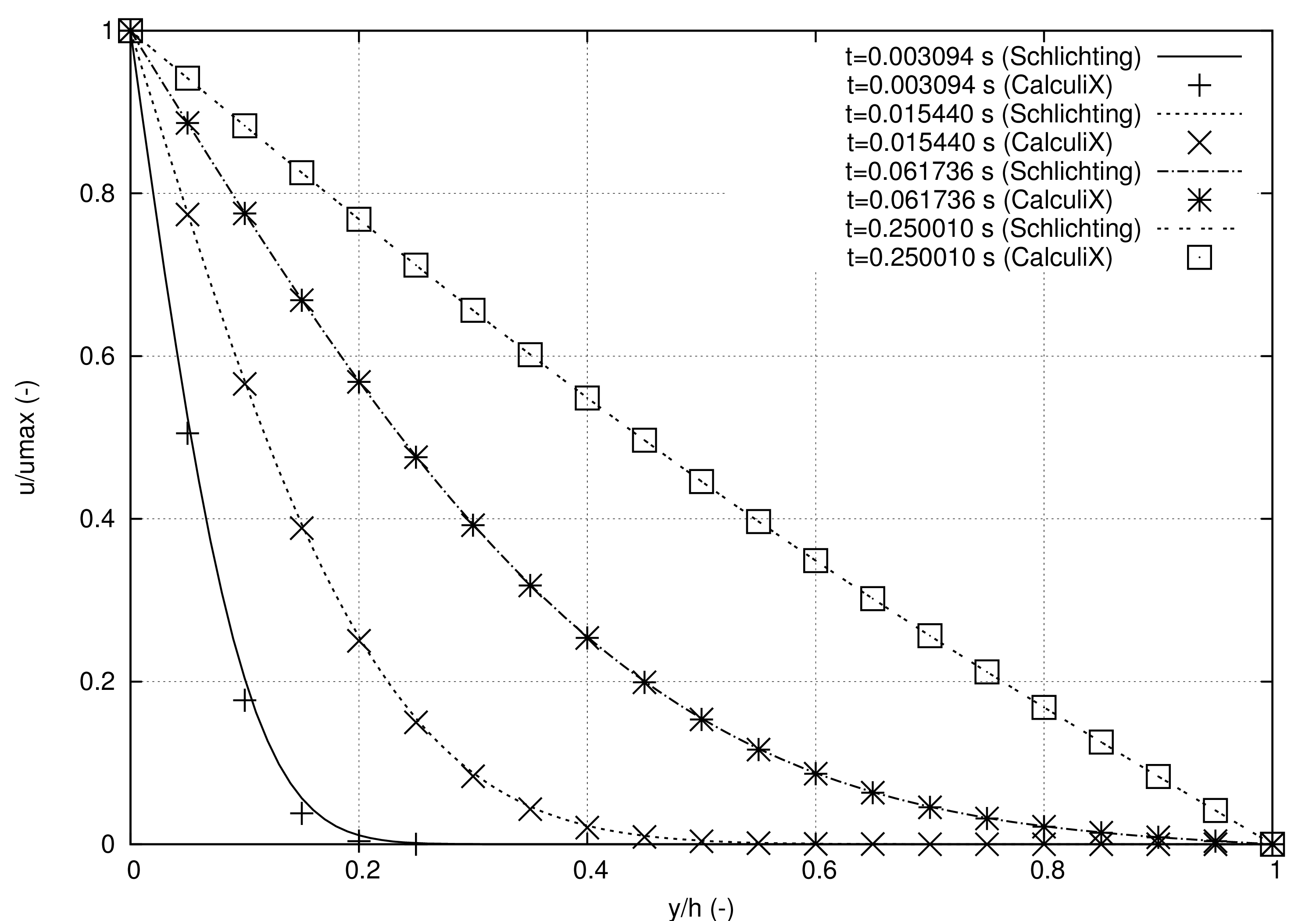
もうひとつの有名な問題は平行板間の非圧縮性層流です。 時間ゼロにおいては板は2枚とも停止していますが、時間が正の数の場合には一方の板がもう一方の板に対して平行な方向に速度1で動きます。 この解析解は[62]にある通りで誤差補正関数erfcを含んだ級数展開の形をしています。 定常状態においては流速は板の間の空間を線形に横切る形をしています。 異なる時間でのそれぞれの流速は図31に示す通りです。図では平板間距離が1で動粘性係数が ν=1 の場合の解析解との比較を行っています。 CalculiXの入力デッキがどうなるかはテストパッケージ(couette1.inp)を見るとわかります。 時間増分を0.00012376とすることで良好な結果が得られます。ただしどうすれば正しい結果を得るための増分を計算できるかは不明なままです。 今のところ適切と言える方法は結果が変わらなくなるまで増分を小さくしていく、というものだけです。 図では数値解と解析解がよく合っていて、CalculiXのCFD実装において時間積分が正しく行われていることが示されています。 進行時間が短い時の小さなずれはメッシュが粗いことに起因します。