定常、層流、非粘性圧縮流体の翼周り流れ

次へ上へ前へ目次へ
次へ：Channel with hydraulic jump 上へ：Simple example problems 前へ：Transient laminar incompressible Couette 目次へ

定常、層流、非粘性圧縮流体の翼周り流れ

このセクションではマッハ数0.95でのNACA012翼の周りの非粘性圧縮流体の層流を扱います。入力デッキ（大規模流体例テストパッケージ内のnaca012_mach0.95_finefine.inpという名前のファイル）は以下のようになります：

*NODE, NSET=Nall
       1,7.600000000000e-04,-1.412800000000e-01,0.000000000000e+00
...
*ELEMENT, TYPE=F3D8, ELSET=Eall
     1,     1, 34101, 39113, 34104, 34109, 34113,140301, 47554
...
MATERIAL,NAME=AIR
*CONDUCTIVITY
5.e-4
*FLUID CONSTANTS
1.,1.e-20,293.
*SPECIFIC GAS CONSTANT
0.285714286d0
*SOLID SECTION,ELSET=Eall,MATERIAL=AIR
*PHYSICAL CONSTANTS,ABSOLUTE ZERO=0.
*INITIAL CONDITIONS,TYPE=FLUID VELOCITY
Nall,1,1.d0
Nall,2,0.d0
Nall,3,0.d0
*INITIAL CONDITIONS,TYPE=PRESSURE
Nall,0.79145232
*INITIAL CONDITIONS,TYPE=TEMPERATURE
Nall,2.77008310
*VALUES AT INFINITY
2.77008310,1,0.79145232,1.,1.
**
*STEP,INCF=100000
*CFD,STEADY STATE,COMPRESSIBLE
1.,1.,,,
*BOUNDARYF
** BOUNDARYF based on in
6401, S6, 11,, 2.770083
...
*DFLUX
** DFlux based on airfoil
309, S2, 0.000000e+00
...
*MASS FLOW
** DFlux based on airfoil
309, M2, 0.000000e+00
...
*NODE FILE,FREQUENCYF=5000
MACH,VF,TSF,PSF,TTF
*END STEP

**図32:** 全体メッシュ
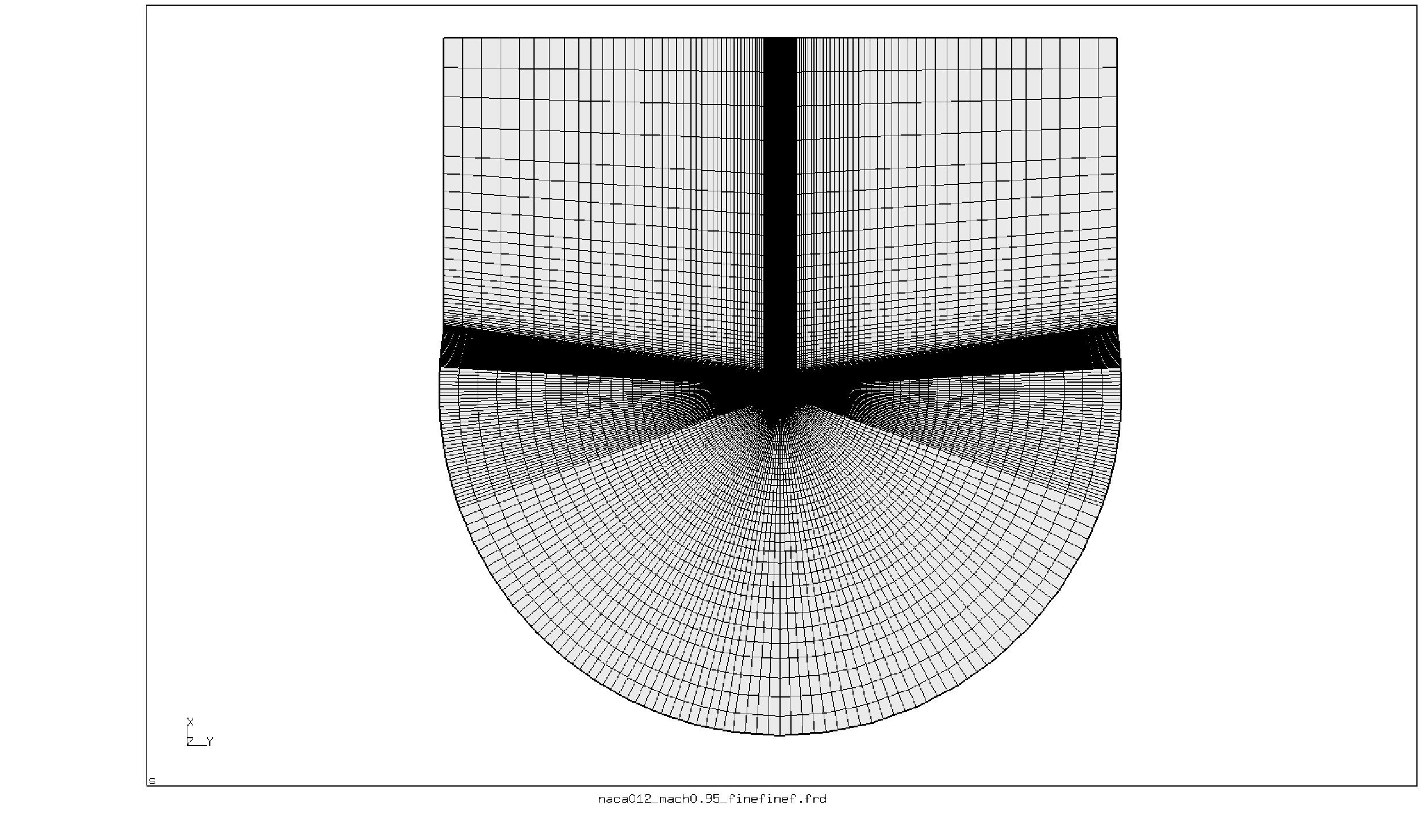
$\begin{figure}\begin{center} \epsfig{file=naca_mesh1.ps,width=8cm}\end{center}\end{figure}$

**図33:** NACA翼周りの詳細メッシュ
$\begin{figure}\begin{center} \epsfig{file=naca_mesh2.ps,width=8cm}\end{center}\end{figure}$

**図34:** マッハ数
$\begin{figure}\begin{center} \epsfig{file=naca_mach.ps,width=8cm}\end{center}\end{figure}$

**図35:** 静圧
$\begin{figure}\begin{center} \epsfig{file=naca_ps.ps,width=8cm}\end{center}\end{figure}$

**図36:** 静温度
$\begin{figure}\begin{center} \epsfig{file=naca_ts.ps,width=8cm}\end{center}\end{figure}$

**図37:** 全温度
$\begin{figure}\begin{center} \epsfig{file=naca_tt.ps,width=8cm}\end{center}\end{figure}$

節点と要素（8節点のブリック要素。これらは内部的には有限体積セルとして扱われます。領域のメッシュと形状については図32と図33を参照）の定義の後、物性が定義されています。定圧 c_p での熱容量は1に規格化され、粘性係数 μ は非常に低い値(10^-20)に設定されているので、流れは摩擦なしの状態です。比気体定数は κ=c_p/c_v=1.4 です。初期条件はX方向の速度が v_x、静圧と静温度の値は密度が ρ=1 かつマッハ数 M=v_x/(μL)=0.95 となるように設定されています。ここでLは翼のX方向の長さでちょうど1です。また流入部には *BOUNDARYF カードで境界条件が設定されています。それ以外の境界条件は翼表面での質量流量ゼロ、Z方向での質量流量ゼロ（流れは2次元流れとしてモデル化されています）、遠方境界部での質量流量ゼロで全て *MASS FLOW カードを使って設定されています。また同じ境界には *DFLUX カードを使って熱流れゼロが設定されています。最後にマッハ数、流速、静温度、静圧、全温度の出力を設定しています。*CFD カードのパラメーターによって流体流れは圧縮性（密度定義は材料カードで要求されたものに従いません）になり、定常状態に到達するまで計算が行われます。これを設定しない場合には、定常状態判定は行われず、計算は *STEP で設定された繰り返し数に到達するまで続けられます。

計算結果は図34、図35、図36、図37に示す通りです。計算は75,000回後に中断されていますが、計算を続ければ最大マッハ数はもう少し増加しそうです。全温度はほぼ一定です。流線に沿った全温度の総変化は以下の式で与えられます：

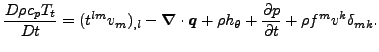$\displaystyle \frac{D \rho c_p T_t}{D t} = (t^{lm} v_m)_{,l} - \boldsymbol{\nab... ... + \rho h_{ \theta} + \frac{\partial p}{\partial t} + \rho f^m v^k \delta_{mk}.$

(1)

右辺の項は粘性の効果（ゼロ）、熱流れ（熱伝導係数が非ゼロなので非ゼロ）、単位質量あたりの熱増加量（ゼロ）、圧力変化（定常状態ではゼロ）、外部体積力の効果（ゼロ）に対応します。

次へ上へ前へ目次へ
次へ：Channel with hydraulic jump 上へ：Simple example problems 前へ：Transient laminar incompressible Couette 目次へ

guido dhondt 2016-03-08