 |
あまり知られていませんが開水路は1次元ネットワークとしてモデル化することができます。 支配方程式はブレス方程式(セクション6.9.18を参照)で、 利用可能な流体セクションタイプはセクション6.6にリストアップされています。
今回の例の入力デッキは以下に示すとおりです。
**** 構造:2つのタンクに繋がった水路 ** テスト対象:急勾配、フロントウォーター - 跳水 - バックウォーターカーブ ** ** *NODE,NSET=NALL 1,0.,0.,0. 2,1.,0.,0. 3,2.,0.,0. 4,3.,0.,0. 5,4.,0.,0. 6,5.,0.,0. 7,6.,0.,0. 8,7.,0.,0. 9,8.,0.,0. 10,9.,0.,0. 11,10.,0.,0. *ELEMENT,TYPE=D,ELSET=EALL 1,0,1,2 2,2,3,4 3,4,5,6 4,6,7,8 5,8,9,10 6,10,11,0 *MATERIAL,NAME=WATER *DENSITY 1000. *FLUID CONSTANTS 4217.,1750.E-6,273. *ELSET,ELSET=E1 1,6 *ELSET,ELSET=E2 2 *ELSET,ELSET=E3 3 *ELSET,ELSET=E4 4 *ELSET,ELSET=E5 5 *FLUID SECTION,ELSET=E1,TYPE=CHANNEL INOUT,MATERIAL=WATER *FLUID SECTION,ELSET=E2,TYPE=CHANNEL SLUICE GATE,MANNING,MATERIAL=WATER 10.,0.005,0.8,,3 *FLUID SECTION,ELSET=E3,TYPE=CHANNEL SLUICE OPENING,MANNING,MATERIAL=WATER 10.,0.005,0.1,0.,0.01,2 *FLUID SECTION,ELSET=E4,TYPE=CHANNEL STRAIGHT,MANNING,MATERIAL=WATER 10.,0.005,49.8,0.,0.01,2 *FLUID SECTION,ELSET=E5,TYPE=CHANNEL RESERVOIR,MANNING,MATERIAL=WATER 10.,0.005,0.1,0.,0.01,2 *BOUNDARY 10,2,2,2.7 *BOUNDARY,MASS FLOW 1,1,1,60000. *STEP *HEAT TRANSFER,STEADY STATE *DLOAD EALL,GRAV,9.81,0.,0.,-1. *NODE PRINT,NSET=NALL U *END STEP
これはCalculiXのテストパッケージにある例のひとつです。水路は長く1列に並んだ6つの3節点ネットワーク要素(タイプD)で構成されます。 節点には仮の座標が設定されています。これらは計算には影響を与えませんが、.frdファイルには出力されます。 CalculiX GraphiXを使って適切な可視化を行うためには、正しい座標を使用したほうが良いでしょう。 通常のネットワークと同様、使用される節点の最後のものと終端要素のラベルはゼロです。 使用する物性は水で、密度、熱容量、粘性係数で定義されます。 次に *FLUID SECTION カードで参照できるように(*ELSET を使用して)要素をそれぞれ適切なセットに設定します。
水路の構造は *FLUID SECTION カードを読むとわかります。 上流側には水門が、下流側には大きなタンクがあり、両者は水路で直線的に結ばれています。 最上流の要素を見ると水門が実際には2つの要素からなっていることがわかります。 実際の水門要素と水路開口部要素です。 これは水門の下端での水深が固定されているにも関わらず、下流の水位で制御された背水曲線によってこの水深が超過するためです。 水門は幅(10 m で、水路に沿って一定です)、 傾斜0.005(これも水路に沿って一定です)、高さ0.8 m によって表されます。 さらに 下流の水門開口部要素の水位も同じように与えられます(3)。 水門開口部開口部要素は同じ幅、傾斜を持ち、長さは0.1です.。 負の値の長さが与えられた場合には節点座標から実際の長さが計算されます。 角度 θ はゼロで、これは断面が長方形であって台形でないことを意味します。 パラメーターMANNINGが *FLUID SECTION カードで使われているので、次のパラメーター(0.01 m-1/3s)はマニング係数です。 最後に上流の水門要素のラベルが与えられます(2)。 直線状の水路要素の定数がセクション6.6で確認できます。 ここで重要なのはその長さが49.8 m だということです。最後の要素、つまりタンクは再び非常に短い要素(長さ0.1 m)になります。水門開口部やタンクの要素の長さは実際の物理的な長さは持たず短くしておく必要があります。
次に境界条件が定義されています。タンクの水深は2.7 m で、質量流量は60000 kg/s です。CalculiXでのネットワーク計算は定常状態での熱伝達計算の特殊例です。 従って *HEAT TRANSFER カードと STEADY STATE カードが使用されます。支配的な力は重力です。
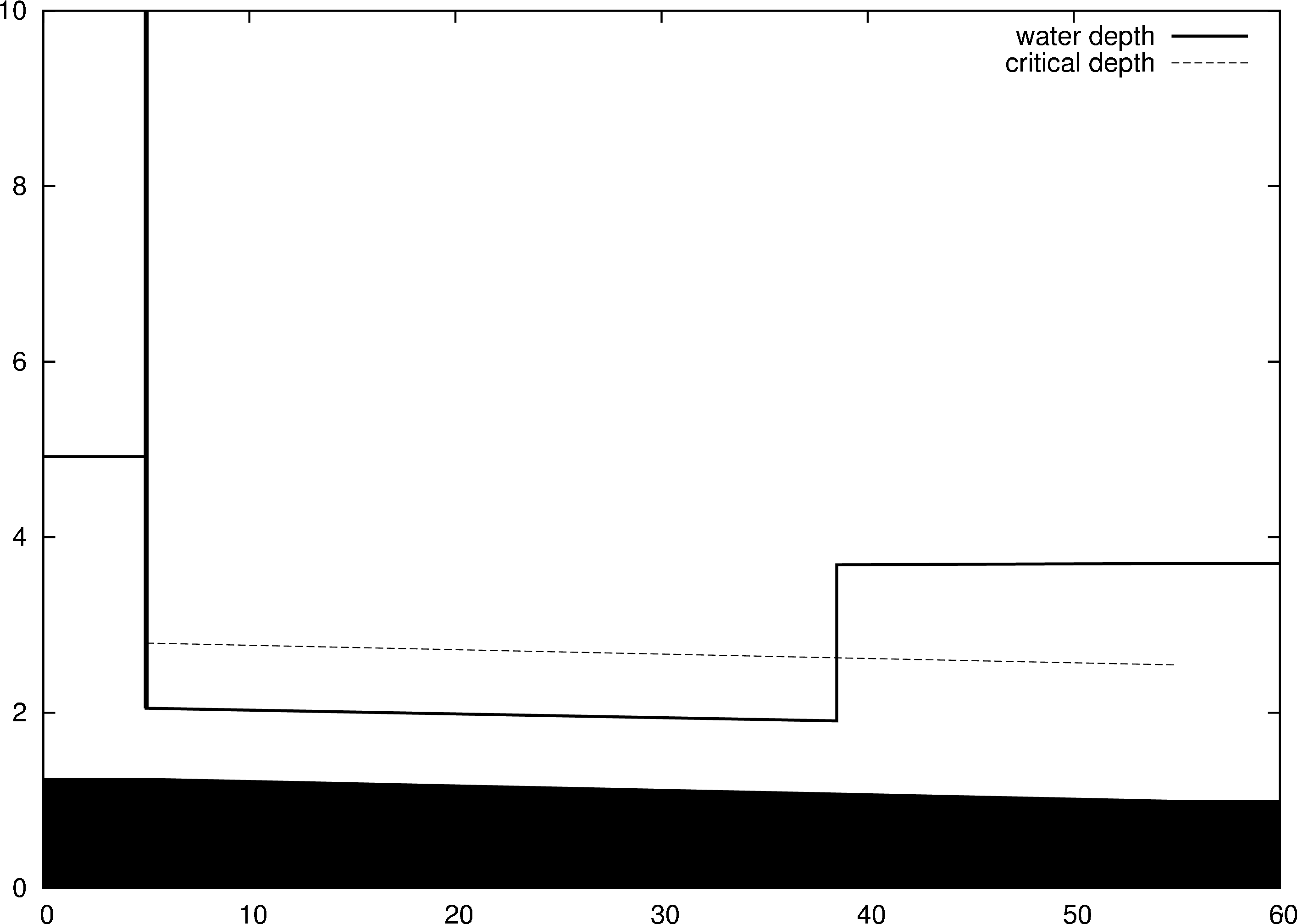
CalculiXを実行すると跳水が要素4(直線状の水路要素)の相対位置0.67に存在するというメッセージが表示されます。 これは図38からも明らかで、ここで水路の水深が深くなります。水門はx=5 m の位置に、タンクはx=55 m の位置にあります。 水路の底部は黒く塗りつぶされています。水門後方の水位は指定されておらず、ある計算の結果では3.667 m になります。水門位置での水位はその高さ0.8 m によって制御されています。 前水曲線(つまり上流の条件 - 水門によって制御される曲線)は下流で発達して、X座標38.5 m にある跳水で背水曲線(つまり下流の条件 - タンクによって制御される曲線)と接続します。 つまり、跳水によって上流の超臨界流れが下流の未臨界流れが繋がれるのです。 臨界深さは図では破線で描かれています。これはフルード数1である臨界流れの深さです。
水路流れでは力学的変位の自由度はそれぞれ質量流量、水深、臨界深さのために使われます。 従って *NODE PRINT カードの下のオプションUによってこれらの情報が.datファイルに出力されます。 また *NODE FILE カードの下でMF、DEPT、HCRIを選択すると同じ情報が.frdファイルに出力されます。