次へ 上へ 前へ 目次へ
次へ：Hydraulic Networks 上へ：Types of analysis 前へ：Diffusion mass transfer in 目次へ


空力ネットワーク

空力ネットワークは、理想気体と見なされる圧縮性媒体で満たされたネットワーク要素を連結して作成されます。理想気体は以下を満たします。

$\displaystyle p=\rho R \theta,$ (239)

ここで p は圧力、ρ は密度、R は特定の気体定数、θ は絶対温度です。ネットワーク要素（セクション6.2.31を参照）は3つの節点から構成されます。端節点では温度と圧力は未知、中間節点では質量流量が未知です。端節点はネットワークの接続点の役割を担い、中間節点は1要素内の流れを表します。これらの未知数を決定するためには3種類の式が利用できます。端節点での質量保存式、エネルギー保存式、中間節点での運動量保存式です。今のところ対応しているのは定常流れだけです。

定常流れにおける圧縮性流体での質量保存則は以下の形で表現されます。

$\displaystyle \mathbf{\nabla} \cdot (\rho \mathbf{v}) = 0$ (240)

ここで v は流速ベクトルです。端節点 i につながる全ての要素にわたって積分を行なうと以下の様になります。

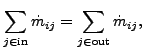$\displaystyle \sum_{j \in \text{in}} \dot{m}_{ij} = \sum_{j \in \text{out}} \dot{m}_{ij},$ (241)

$ \dot{m}_{ij}$は節点 i と 節点 j の間の質量流れです。上式では$ \dot{m}_{ij}$は常に正です。

運動量保存や要素方程式は要素の流体セクションタイプ属性によって異なり、詳しくは流体セクションについてのセクション6.4で説明されています。端節点 i, j を持つ要素では、一般に$ f({p_{tot}}_i, {\theta_{tot}}_i, \dot{m}_{ij},{p_{tot}}_j)=0$（正の$ \dot{m}_{ij}$の場合。p は全圧、$ \theta_{tot}$は全温度）という形をとりますが、さらに複雑な関係をとる場合もあります。この式の中に温度が現れるという点には特に注意してください（水力ネットワークの場合にはそうなりません）。

定常状態でのエネルギー保存式から以下のような式が導かれます（[25]）。

$\displaystyle \mathbf{\nabla} \cdot (\rho h_{tot} \mathbf{v}) = - \mathbf{\nabla} \cdot \mathbf{q} + \rho h^{\theta} + \rho \mathbf{f} \cdot \mathbf{v},$ (242)

ここで q は外部の熱フラックス、$ h^{\theta}$は単位質量あたりの体積フラックス、f は単位質量あたりの体積力です。また$ h_{tot}$は全エンタルピーで以下を満たします。

$\displaystyle h_{tot} = c_p \theta + \frac{\mathbf{v} \cdot \mathbf{v}}{2},$ (243)

ここで cp は定圧比熱、θ は絶対温度（ケルビン温度）です。後者の式は cp が温度に対して独立であるという仮定の時のみ適用されます。産業的な多くの問題ではこれが当てあはまります。これに関しては全温度と全圧（それぞれ、よどみ温度、よどみ圧力とも呼ばれます）の定義を思い出してください。

$\displaystyle \theta_{tot} = \theta + \frac{\mathbf{v} \cdot \mathbf{v}}{2 c_p},$ (244)

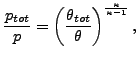$\displaystyle \frac{p_{tot}}{p} = \left(\frac{\theta_{tot}}{\theta} \right) ^ {\frac{\kappa}{\kappa-1}},$ (245)

ここで$ \kappa = c_p/c_v$です。θ と p はそれぞれ静温度、静圧とも呼ばれます。

要素の端節点が大きなチャンバーと仮定できる場合は、流速 v はゼロになります。この場合には全ての量が静的なものになり、終端節点 i に属する全ての要素にわたってエネルギー方程式を積分した結果は以下の様になります。

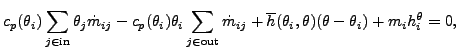$\displaystyle c_p (\theta_i) \sum_{j \in \text{in}} \theta_j \dot{m}_{ij} - c_p... ...{ij} + \overline{h}(\theta_i, \theta) (\theta - \theta_i) + m_i h_i^{\theta}=0,$ (246)

ここで$ \overline{h}(\theta_i,\theta)$は壁に対する対流係数です。これは現実的に正しいものではありませんが、cp に対するわずかな温度依存性があることに注意してください。ある節点に流入する全ての流れが同時に流出しなければならず、両方ともが流入する流れの平均温度値と対応する cp を持つとすると、以下の様になります。

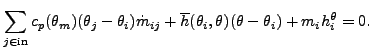$\displaystyle \sum_{j \in \text{in}} c_p (\theta_m) (\theta_j-\theta_i) \dot{m}_{ij} + \overline{h}(\theta_i, \theta) (\theta - \theta_i) + m_i h_i^{\theta}=0.$ (247)

ここで$ \theta_m=(\theta_i+\theta_j)/2$です。

空力ネットワークの計算は *HEAT TRANSFER キーワード・カードによって有効になります。このようなネットワークでは固体力学的な熱伝達計算のための対流境界条件が必要になることが多いですが、ネットワーク計算では独自に実行を行なうことができます。

ネットワークを使う場合にとりわけ注意しなければいけないのは、一意な買いを得るために必要な境界条件の数です。方程式が未知数よりも多かったり少なかったりする事態にならないよう、以下の規則を守る必要があります。

出力変数は質量流量（*NODE PRINT カードまたは*NODE FILEカードのMFキー）、全圧（*NODE PRINT カードのPNキー……Network Pressure…… と*NODE FILE カードのPTキー）、全温度（*NODE PRINT カードのNTキー、*NODE FILE カードのTTキー）です。*NODE PRINT キーワードのラベルはより一般的なもので、*NODE FILE キーワードのものはより詳細なものであることに注意してください。これら変数はネットワークにおける主要変数です。さらにユーザーは静温度（*NODE FILE カードのTSキー）を出力することも可能です。内部的には、ネットワーク節点では変位場の第1成分から第3成分がそれぞれ質量流量、全圧、静温度に使用されています。従って *NODE PRINT カードで U を使用しても出力を行なうことが可能です。

次へ 上へ 前へ 目次へ
次へ：Hydraulic Networks 上へ：Types of analysis 前へ：Diffusion mass transfer in 目次へ
guido dhondt 2016-03-08