| (199) |
*HEAT TRANSFER プロシージャ・カードによって有効化される熱伝達解析では温度が独立自由度になります。本質的に言うと温度とフラックス境界条件の支配下にあるエネルギー方程式が解かれるということになります([18])。定常状態計算ではこれはラプラス型の方程式になります。
熱伝達の支配方程式は以下の様になります。
| (199) |
ここで κ は伝導係数、ρ は密度、h は単位質量当たりの発熱、c は比熱です。
温度は *BOUNDARY カードの自由度11を使用して定義できます。フラックス型の境界条件は以下の組み合わせからなります。
| (200) |
ここで q は面に対するフラックスの法線、h は境膜係数、T は物体温度、T0 は環境温度(シンク温度とも呼ばれます)です。CalculiXでは強制対流計算を行なうこともできます。シンク温度が未知の場合でも可能です。流体や気体によって表面冷却を行なうような問題ではこれを使用できます。
| (201) |
ここでqは面に対するフラックスの法線、εは輻射率、θ は絶対物体温度(ケルビン温度)、θ0 は絶対環境温度(シンク温度とも呼ばれます)。輻射率は0から1の間の値をとります。物体に対して値ゼロを設定すると吸収も輻射も起きず100%反射されます。値1を設定すると黒体になります。輻射は(輻射方向に依存しない)拡散、(輻射の波長に依存しない)灰色と仮定されています。またCalculiXでは複数の面の間の輻射相互作用をシミュレートする空洞輻射も使用可能です。この場合には形態係数が計算されます。熱伝達の基礎に関しては[34]を、形態係数計算の基礎については[6]を参照してください。
形態係数の計算では4重積分が必要になります。ランベルの解析式を使用するとこの積分は2重積分に減らせます。現在、CalculiXはこれを使用しています。相互作用面は3角形面に分割され、2つの3角形の間の形態係数が計算されるのです。これにはベース3角形(の重心)での1点積分とベース3角形周りの半球を覆う他の3角形全体を積分範囲とする解析式が使用されます。radmatrixサブルーチンの変数「factor」の値を増やすことでベース3角形での積分の精度を上げることができます。このサブルーチンのコメントを参照してください。ただし精度を上げると計算時間は長くなります。
熱伝達解析では材料の伝導係数(*CONDUCTIVITYを使用)が必要で、それが非定常計算の場合には熱容量(*SPECIFIC HEATを使用)が必要になります。さらに輻射境界条件では *PHYSICAL CONSTANTS カードが必要で、ここでユーザーのスケールの絶対ゼロ点とボルツマン定数を指定します。
比熱の局所急最大によって相転移をモデル化できることに注意してください。完全相転移では単位質量当たりのエネルギー U が以下を満足する必要があります。
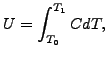 |
(202) |
ここで C は比熱、[T0, T1] は相転移が起きる温度範囲です。