次へ 上へ 前へ 目次へ
次へ：Convergence criteria 上へ：Types of analysis 前へ：Substructure Generation 目次へ


電磁気力

CalculiX では一部の種類の電磁気計算を行なうことが可能です。可能な計算には以下が含まれます。

このセクションでは上記のうちの後の2つのみを取り上げます。支配方程式であるマクスウェル方程式は以下の様になります（変位電流項は式266で消去されます）。

$\displaystyle \nabla \cdot \boldsymbol{D} = \rho$ (263)

$\displaystyle \nabla \times \boldsymbol{E} = - \frac {\partial \boldsymbol{B}}{\partial t}$ (264)

$\displaystyle \nabla \cdot \boldsymbol{B} = 0$ (265)

$\displaystyle \nabla \times \boldsymbol{H} = \boldsymbol{j}$ (266)

ここで E は電場、D は電気変位場、B は磁場、H は磁場強度、j は電流密度、ρ は電荷密度です。これらの場は以下の構成方程式で互いにつながっています。

$\displaystyle \boldsymbol{D} = \epsilon \boldsymbol{E}$ (267)

$\displaystyle \boldsymbol{B} = \mu \boldsymbol{H}$ (268)

$\displaystyle \boldsymbol{j} = \sigma \boldsymbol{E}.$ (269)

ここで ε は誘電率、μ は透磁率、σ は電気伝導度です。今考えている問題では ε と D は不要で、式（263）は消去することができます。これらの関係は線形・等方性と仮定されていますが、材料パラメーターには温度依存性を持たせることができます。またヒステリシスは考慮されておらず、基本的には常磁性材料、反磁性材料のみが考慮されています。今のところ、強磁性材料は使用できません。

電磁気力を扱うため追加の基礎単位としてアンペア（A)）が必要になります。他の諸量はSI単位系 A、m、s、kg、K を使って書き表すことができますが、組み立て単位もよく使われます。これらの単位をまとめると表17の様になります。

表 17:電磁気問題でよく使われる単位
記号 意味 単位
I 電流 A
E 電場 $ \frac{\text{V}}{\text{m}} = \frac{\text{kg}.\text{m}}{\text{A}.\text{s}^3}$
D 電気変位場 $ \frac{\text{C}}{\text{m}^2} = \frac{\text{A}.\text{s}}{\text{m}^2}$
B 磁場 $ {\text{T}} = \frac{\text{kg}}{\text{A}.\text{s}^2}$
H 磁場強度 $ \frac{\text{A}}{\text{m}}$
j 電流密度 $ \frac{\text{A}}{\text{m}^2}$
ε 誘電率 $ \frac{\text{F}}{\text{m}} = \frac{\text{A}^2\text{s}^4}{\text{kg}\text{m}^3}$
μ 透磁率 $ \frac{\text{kg}.\text{m}}{\text{A}^2.\text{s}^2}$
σ 電気伝導度 $ \frac{\text{S}}{\text{m}}=\frac{\text{A}^2.\text{s}^3}{\text{kg}.\text{m}^3}$
P 磁位 A
V 電位 V$ = \frac{\text{kg}.\text{m}^2}{\text{A}.\text{s}^3}$
A ベクトル磁気ポテンシャル $ \frac{\text{kg}.\text{m}}{\text{A}.\text{s}^2}$

以下では[65]と[36]を参照しています。誘導加熱問題では加熱される物体（＝試料）、周囲の空気、誘導を起こすための電流を供給するコイルから問題が構成されます。コイルに関しては系から分離された、フィードバックを受けない駆動力と仮定できるとします。つまり任意の外部からの影響に対してユーザーが意図したとおりの電流となるように反作用を加える整流装置がコイルには備わっているとします。

図120: 単連結物体の電磁気的構成
\begin{figure}\epsfig{file=em1.eps,width=10cm}\end{figure}

まず物理的に何が起きるのかを理解することにしましょう。もっとも単純な場合、解析対象は図120のような空気に囲まれた単連結物体から構成されます。物体が単連結であるとは、物体内の仮想的な任意の閉ループを物体内から出ることなく、1点に収束させることができるということを指します。例えば球は単連結ですが、円は単連結ではありません。電流を供給するコイルは空気の中に位置しています。電流を流すと式（266）によって磁場強度場が、式（268）によって磁場が、空気中と物体内のいたるところに生まれます。電流が時間変化しない場合には、これで問題の状況ができあがります。

電流が時間変化する場合には、磁場も時間変化し、式（264）によっていたるところに電場が生まれます。この電場は式（269）によって任意の電気伝導物体の中、つまり空気を除く物体の中に電流（渦電流と呼ばれます）を生み出します。さらにこの電流は式（266）に基づいて元の磁場強度場とは反対の向きの磁場強度場を生み出します。以上の様にして渦電流は物体内での磁場の生成を抑えます。つまり物体内では磁場は瞬時には立ち上がらないのです。むしろ熱伝達によって物体の温度が次第に変化するように、磁場は次第に変化します。実際問題として、この2つの現象はどちらも時間に関して1次の微分方程式として表現されます。渦電流のオーム損失は熱発生源となり、産業上の誘電加熱問題で扱われます。

以上の考察から、物体内（図120の領域2。[65]とは領域1、領域2が入れ替わっていることに注意してください。）では電気と磁気の両方が計算されている一方で、空気中（領域1）では磁場だけを考えればいいことに気がつきます。従って空気中では以下を満足するスカラー磁気ポテンシャルを使用するだけで十分なのです。

$\displaystyle \boldsymbol{H}=\boldsymbol{T_0} - \nabla P.$ (270)

ここで T0 は無限自由空間内のコイル電流によって起きる磁場強度です。T0 はビオ・サバールの関係[22]を使用して計算することが可能です。物体内の場は以下を満足するベクトル磁気ポテンシャル A とスカラー電気ポテンシャル V によって書き表すことができます。

$\displaystyle \boldsymbol{B}= \nabla \times \boldsymbol{A},$ (271)

$\displaystyle \boldsymbol{E}= -\frac{\partial \boldsymbol{A}}{\partial t} - \nabla V.$ (272)

実際には$ V=\frac{\partial v}{\partial t}$とするのが便利で、以下の様になります。

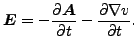$\displaystyle \boldsymbol{E}= -\frac{\partial \boldsymbol{A}}{\partial t} -\frac{\partial \nabla v}{\partial t}.$ (273)

これによって結果行列が対称になることが保証されます。

図121: 多重連結領域の電磁気的構成
\begin{figure}\epsfig{file=em2.eps,width=10cm}\end{figure}

物体が多重連結領域の場合、計算領域は3つの領域で構成されます。この場合でも（複数の）物体は A と V で管理される領域2からなりますが、空気は2つの部品に分解されます。ひとつは物体に追加された場合にそれらと単連結になります。これを領域3でベクトル磁気ポテンシャル A によって記述されます。領域3には電流の流れているコイルは存在しないと仮定されています。残る空気部部が領域1で、これはスカラー磁気ポテンシャル P で書き表されます。

それぞれの領域では、それぞれ異なる方程式が解かれます。領域1では電気伝導がないので電場は重要ではありません。従って磁場を解くだけで十分であり、式（265）と式（266）だけが満たされます。式（270）の仮定を使用すると、式（266）は自動的に満たされます。T0 によって満たされ、勾配の回転が消えるためです。これによって次の式が得られます。

$\displaystyle \nabla \cdot \mu (\boldsymbol{T_0} - \nabla P) = 0.$ (274)

領域2では式（264）、式（265）、式（266）が満たされなければならず、式（271）、式（272）による方法が使われます。式（272）の回転を取ると式（264）が得られ、式（271）の発散を取ると式（265）が得られます。また式（271）と式（272）を式（266）に代入すると以下が得られます。

$\displaystyle \nabla \times \frac{1}{\mu } (\nabla \times \boldsymbol{A}) + \sigma \frac{\partial \boldsymbol{A} }{\partial t} + \sigma \nabla V = 0.$ (275)

ベクトル磁気ポテンシャル A は式（271）からは一意に定義されません。また A の発散は自由に定義できます。ここでは以下の様なクーロンゲージを使用します。

$\displaystyle \nabla \cdot \boldsymbol{A}=0.$ (276)

式（266）が満たされと自動的に電荷の保存が満足されます。集中電荷がないため領域2では以下のようなることに注意してください。

$\displaystyle \nabla \cdot \boldsymbol{j} =0,$ (277)

以上から単連結物体では式（274）（領域1）、式（275）（領域2）、式（276）（領域2）が得られます。実際には式（275）と式（276）は統合されて以下の様に扱われることが多いです。

$\displaystyle \nabla \times \frac{1}{\mu } (\nabla \times \boldsymbol{A}) - \na... ...{A} + \sigma \frac{\partial \boldsymbol{A} }{\partial t} + \sigma \nabla V = 0.$ (278)

ただし、この場合には式（266）の解とは同等にならず、式（277）が明示的に満たされなければならなくなります。

$\displaystyle \nabla \cdot \sigma (\frac{\partial \boldsymbol{A} }{\partial t} + \nabla V) = 0.$ (279)

結果、解かれる方程式は式（278）（領域2）、式（279）（領域2）、式（274）（領域1）となります。

領域3では満たされなければならないのは式（265）と j = 0 での式（266）だけになります（コイルは領域1にあるとします）。式（271）の仮定を使用すると、式（265）は自動的に満たされ、式（266）は以下の様になります。

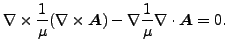$\displaystyle \nabla \times \frac{1}{\mu } (\nabla \times \boldsymbol{A}) - \nabla \frac{1}{\mu } \nabla \cdot \boldsymbol{A} = 0.$ (280)

領域境界での境界条件は以下の様になる必要があります。

$\displaystyle \boldsymbol{B_1} \cdot \boldsymbol{n_1} + \boldsymbol{B_2} \cdot \boldsymbol{n_2} = 0,$ (281)

$\displaystyle \boldsymbol{H_1} \times \boldsymbol{n_1} + \boldsymbol{H_2} \times \boldsymbol{n_2} = 0$ (282)

$\displaystyle \boldsymbol{j_2} \cdot \boldsymbol{n_2}= 0$ (283)

以上の全てが Γ12 上で満足されなければなりません。ベクトル磁気ポテンシャル項 A では、スカラー電気ポテンシャル V とスカラー磁気ポテンシャル P は Γ12 上で以下を満たします。

$\displaystyle \mu (\boldsymbol{T_0} - \nabla P) \cdot \boldsymbol{n_1} + (\nabla \times \boldsymbol{A}) \cdot \boldsymbol{n_2} =0,$ (284)

$\displaystyle (\boldsymbol{T_0} - \nabla P) \times \boldsymbol{n_1} + \frac{1}{\mu _1} (\nabla \times \boldsymbol{A}) \times \boldsymbol{n_2} = 0$ (285)

$\displaystyle (\frac{\partial \boldsymbol{A} }{\partial t} + \nabla V)_2 \cdot \boldsymbol{n_2} = 0$ (286)

一意な解を得るためには電気ポテンシャルが1節点で固定され、A の法線成分が Γ12 に沿ってゼロにならなければいけません[65]。

$\displaystyle \boldsymbol{A} \cdot \boldsymbol{n_2}=0.$ (287)

上式の弱形式を得るために、式に試行関数をかけ、さらに積分します。試行関数は δA、δV と δP で記述されます。式（278）から開始して、δA をかけて、以下のベクトル恒等式を使用します。

$\displaystyle \nabla \cdot (\boldsymbol{a} \times \boldsymbol{b})=(\nabla \time... ...{a}) \cdot \boldsymbol{b} - \boldsymbol{a} \cdot (\nabla \times \boldsymbol{b})$ (288)

$\displaystyle \nabla \cdot (\alpha \boldsymbol{a}) = \nabla \alpha \cdot \boldsymbol{a} + \alpha \nabla \cdot \boldsymbol{a}$ (289)

すると以下の様になります（ひとつ目のベクトル恒等式で$ \boldsymbol{b}= (\nabla \times \boldsymbol{A})/\mu $とします）。

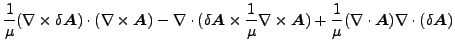$\displaystyle \frac{1}{\mu } (\nabla \times \delta \boldsymbol{A}) \cdot (\nabl... ...rac{1}{\mu } (\nabla \cdot \boldsymbol{A}) \nabla \cdot (\delta \boldsymbol{A})$
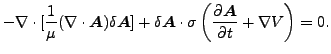$\displaystyle - \nabla \cdot [ \frac{1}{\mu } (\nabla \cdot \boldsymbol{A}) \d... ...igma \left(\frac{\partial \boldsymbol{A} }{\partial t} + \nabla V \right) = 0.$ (290)

さらに（Ω2 は自由境界を持たない、つまり Ω1 に連結していない境界は存在しないと仮定して）ガウスの定理を使用して積分を行なうと以下の様になります。

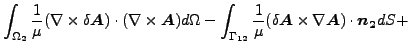$\displaystyle \int _{\Omega _2} \frac{1}{\mu } (\nabla \times \delta \boldsymbo... ...\delta \boldsymbol{A} \times \nabla \boldsymbol{A}) \cdot \boldsymbol{n_2} dS +$
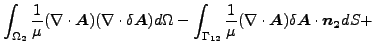$\displaystyle \int _{\Omega _2} \frac{1}{\mu } (\nabla \cdot \boldsymbol{A}) (... ...(\nabla \cdot \boldsymbol{A}) \delta \boldsymbol{A} \cdot \boldsymbol{n_2} dS +$
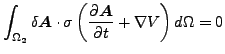$\displaystyle \int _{\Omega _2} \delta \boldsymbol{A} \cdot \sigma \left(\frac{\partial \boldsymbol{A} }{\partial t } + \nabla V \right) d \Omega =0$ (291)

また試行関数は力学的拘束を満足しなければなりません。従って δA・n2 = 0 、2番目の表面積分はゼロとなります。

またベクトル恒等式

$\displaystyle (\boldsymbol{a} \times \boldsymbol{b}) \cdot \boldsymbol{n} = \boldsymbol{a} \cdot (\boldsymbol{b} \times \boldsymbol{n})$ (292)

と式（285）による境界条件を適用すると、1番目の表面積分の被積分関数は以下の様に書けます。

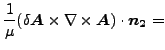$\displaystyle \frac{1}{\mu } (\delta \boldsymbol{A} \times \nabla \times \boldsymbol{A}) \cdot \boldsymbol{n_2} =$
$\displaystyle \frac{1}{\mu } \left (\delta \boldsymbol{A} \cdot [ (\nabla \times \boldsymbol{A}) \times \boldsymbol{n_2}] \right) =$
$\displaystyle - \delta \boldsymbol{A} \cdot \left[ (\boldsymbol{T_0} - \nabla \boldsymbol{P}) \times \boldsymbol{n_1} \right].$ (293)

すると積分は以下の様になります。

$\displaystyle \int _{\Gamma _{12}} \left[ - \delta \boldsymbol{A} \cdot (\bold... ...) + \delta \boldsymbol{A} \cdot (\nabla P \times \boldsymbol{n_2}) \right] dS.$ (294)

さらに上記と同じベクトル恒等式を適用すると次の様になります。

$\displaystyle \int _{\Gamma _{12}} \left[ - \delta \boldsymbol{A} \cdot (\bold... ...) + \boldsymbol{n_2} \cdot (\delta \boldsymbol{A} \times \nabla P) \right] dS.$ (295)

最後に、ベクトル恒等式

$\displaystyle \boldsymbol{n_2} \cdot (\delta \boldsymbol{A} \times \nabla P) = ... ...ldsymbol{A})]-\boldsymbol{n_2} \cdot [ \nabla \times (P \delta \boldsymbol{A})]$ (296)

を使用すると、以下が得られます。

$\displaystyle \int _{\Gamma _{12}} \left\{ - \delta \boldsymbol{A} \cdot (\bol... ...\boldsymbol{n_2} \cdot [ \nabla \times (P \delta \boldsymbol{A}) ] \right\} dS.$ (297)

表面が閉じている場合にはストークスの定理によって最後の積分は消えます。

さて、2番目の方程式である式（279）を見てみましょう。δV をかけると、以下の様に書き直すことができます。

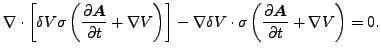$\displaystyle \nabla \cdot \left[ \delta V \sigma \left(\frac{\partial \boldsy... ...igma \left(\frac{\partial \boldsymbol{A} }{\partial t} + \nabla V \right) = 0.$ (298)

積分後、ガウスの定理を適用すると式（286）による境界条件から最後の項のみが残ります。

同様に3番目の方程式、式（274）は以下の様になります。

$\displaystyle \nabla \cdot (\delta P \mu [ \boldsymbol{T_0} - \nabla P])-\nabla \delta P \cdot \mu (\boldsymbol{T_0} - \mu \nabla P) =0.$ (299)

さらに（外部面 Ω1 、つまり Ω2 にも Ω3 にも連結しておらず、条件 B・n1 = 0 が適用されている面で）積分すると次の様になります

$\displaystyle \int _{\Omega _1} \nabla \delta P \cdot \mu (\boldsymbol{T_0} - ... ...{12}} \delta P \mu (\boldsymbol{T_0} - \nabla P] \cdot \boldsymbol{n_1} dS =0.$ (300)

さらに式（284）による境界条件を適用すると以下の様になります。

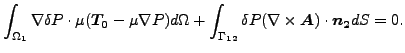$\displaystyle \int _{\Omega _1} \nabla \delta P \cdot \mu (\boldsymbol{T_0} - ... ...ma _{12}} \delta P (\nabla \times \boldsymbol{A}) \cdot \boldsymbol{n_2} dS =0.$ (301)

以上から最終的に得られる支配方程式は次の様になります。

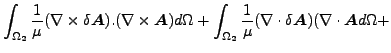$\displaystyle \int _ {\Omega_2} \frac{1}{\mu } (\nabla \times \delta \boldsymbo... ...} (\nabla \cdot \delta \boldsymbol{A}) (\nabla \cdot \boldsymbol{A} d \Omega +$
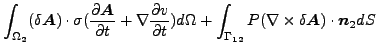$\displaystyle \int _{\Omega _2} (\delta \boldsymbol{A}) \cdot \sigma (\frac{\p... ...amma _{12}} P (\nabla \times \delta \boldsymbol{A}) \cdot \boldsymbol{n}_2 d S$
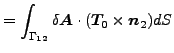$\displaystyle = \int _{\Gamma _{12}} \delta \boldsymbol{A} \cdot (\boldsymbol{T_0 } \times \boldsymbol{n }_2) d S$ (302)

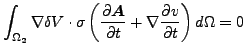$\displaystyle \int _ {\Omega _2} \nabla \delta V \cdot \sigma \left (\frac{\pa... ...mbol{A} }{\partial t} + \nabla \frac{\partial v}{\partial t}\right)d \Omega =0$ (303)

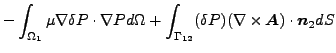$\displaystyle - \int _{\Omega _1} \mu \nabla \delta P \cdot \nabla P d \Omega +... ...mma _{12}} (\delta P) (\nabla \times \boldsymbol{A}) \cdot \boldsymbol{n}_2 d S$
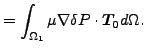$\displaystyle = \int _{\Omega _1} \mu \nabla \delta P \cdot \boldsymbol{T_0} d \Omega.$ (304)

標準経常関数を使うと次の様になります（[18]の第2章を参照）。

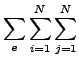$\displaystyle \sum _e \sum _{i=1}^N \sum _{j=1}^N$ $\displaystyle \left\{ \left[ \int _{{V_{0e}}_2} \varphi _{i,L} \frac{1}{\mu } \varphi _{j,L} \delta _{KM} d V_e \right] \delta A_{iK} A_{jM} - \right.$
$\displaystyle \left[ \int _{{V_{0e}}_2} \varphi _{i,M} \frac{1}{\mu } \varphi _{j,K} d V_e \right] \delta A_{iK} A_{jM} +$
$\displaystyle \left[ \int _{{V_{0e}}_2} \varphi _{i,K} \frac{1}{\mu } \varphi _{j,M} d V_e \right] \delta A_{iK} A_{jM} +$
$\displaystyle \left[ \int _{{V_{0e}}_2} \varphi _{i} \sigma \varphi _j dV_e \delta _{KM} \right] \delta A_{iK} \frac{D A_{jM}}{t} +$
$\displaystyle \left[ \int _{{V_{0e}}_2} \varphi _{i} \sigma \varphi _{j,K} dV_e \right] \delta A_{iK} \frac{Dv_j}{Dt} +$
$\displaystyle \left. \left[ \int _{{A_{0e}}_{12}} e_{KLM} \varphi _i \varphi _{j,L} n_{2K} dA_e \right] \delta A_{jM} P_i \right \} =$
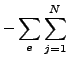$\displaystyle -\sum_e \sum_{j=1}^N$ $\displaystyle \left[ \int _{{A_{0e}}_{12}} e_{KLM} \varphi _j T_{0L} n_{2K} dA_e \right] \delta A_{jM}$ (305)

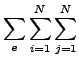$\displaystyle \sum _e \sum _{i=1}^N \sum _{j=1}^N$ $\displaystyle \left\{ \left[ \int _{{V_{0e}}_2} \varphi _{i,K} \sigma \varphi _i dV_e \right] \delta v_j \frac{DA_{iK}}{Dt} \right.$
$\displaystyle \left. \left[ \int _{{V_{0e}}_2} \varphi _{i,K} \sigma \varphi _{j,K} dV_e \right] \delta v_i \frac{Dv_j}{Dt} \right \} = 0$ (306)

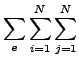$\displaystyle \sum _e \sum _{i=1}^N \sum _{j=1}^N$ $\displaystyle \left\{ \left[ \int _{{V_{0e}}_1} \varphi _{i,K} \mu \varphi _{j,K} dV_e \right] \delta P_i P_j \right.$ (307)
$\displaystyle \left. \left[ \int _{{A_{0e}}_{12}} \varphi _i e_{KLM} \varphi _{j,L} n_{2K} dA_e \right] \delta P_i A_{jM} \right \}$ (308)
$\displaystyle = - \sum_e \sum_i$ $\displaystyle \left[ \int _{{V_{0e}}_1} \mu \varphi _{i,K} T_{0K} dV_e \right] \delta P_i.$ (309)

初めの2つの式は領域2に、最後の式は領域1に適用されることに注意してください。領域3ではひとつ目の式のみが適用され、時間依存項は消去されます。

これによって以下の行列が導出されます。

$\displaystyle [K_{AA}]_{e(iK)(jM)}=\int_{{(V_{0e})}_{\Omega _2}} \frac{1}{\mu }... ...L} \delta_{KM} - \varphi_{i,M} \varphi_{j,K} + \varphi_{i,K} \varphi_{j,M}]dV_e$ (310)

$\displaystyle [K_{AP}]_{e(jM)(i)}=\int_{{(A_{0e})}_{\Gamma _{12}}} e_{KLM} \varphi_i \varphi_{j,L} n_{1K} dA_e$ (311)

$\displaystyle [K_{PA}]_{e(i)(jM)}=\int_{{(A_{0e})}_{\Gamma _{12}}} e_{KLM} \varphi_i \varphi_{j,L} n_{1K} dA_e$ (312)

$\displaystyle [K_{PP}]_{e(i)(j)}=- \int_{{(V_{0e})}_{\Omega _1}} \mu \varphi_{i,K} \varphi_{j,K} dV_e$ (313)

$\displaystyle [M_{AA}]_{e(iK)(jM)}=\int_{{(V_{0e})}_{\Omega _2}} \varphi_i \sigma \varphi_j \delta_{KM} dV_e$ (314)

$\displaystyle [M_{Av}]_{e(iK)(j)}=\int_{{(V_{0e})}_{\Omega _2}} \varphi_i \sigma \varphi_{j,K} \delta_{KM} dV_e$ (315)

$\displaystyle [M_{vA}]_{e(j)(iK)}=\int_{{(V_{0e})}_{\Omega _2}} \varphi_{j,K} \sigma \varphi_i \delta_{KM} dV_e$ (316)

$\displaystyle [M_{vv}]_{e(i)(j)}=\int_{{(V_{0e})}_{\Omega _2}} \varphi_{i,K} \sigma \varphi_{i,K} \delta_{KM} dV_e$ (317)

$\displaystyle \{F_{A}\}_{e(jM)}=- \int_{{(A_{0e})}_{\Gamma _{12}}} e_{KLM} \varphi_j T_{0L} n_{1K} dA_e$ (318)

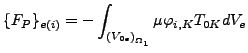$\displaystyle \{F_{P}\}_{e(i)}=- \int_{{(V_{0e})}_{\Omega _1}} \mu \varphi_{i,K} T_{0K} dV_e$ (319)

図122: 支配行列の非ゼロ部分
\begin{figure}\epsfig{file=indmatrix.eps,width=12cm}\end{figure}

繰り返されている添え字は和を取ることを意味しています。行列 [K] は熱伝達解析での熱伝導行列と同等のもの、行列 [M] は熱容量行列に対応するものです。{F} は力を表しています。結果の系は時間に対する1次常微分方程式と対応する図122の様な行列から構成されます。系の解は A、v、p の解となり、これから磁場 B と電場 E が式（271、272）を使用して決定されます。

結果、内部の電磁力は以下の様になります。

$\displaystyle \{F_A\}_{(iK)}$ $\displaystyle = [K_{AA}]_{e(iK)(jM)} \cdot \{A\}_{(jM)} + [K_{AP}]_{e(iK)(j)} \cdot \{P\}_{(j)}$
$\displaystyle = \frac{1}{\mu } \int _{{(V_{0e})}_{\Omega _2}} [\varphi_{i,L} A_{K,L} - \varphi_{i,M} A_{M,K} + \varphi_{i,K} A_{M,M}]dV_e$
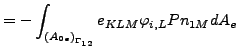$\displaystyle = - \int_{{(A_{0e})}_{\Gamma _{12}}} e_{KLM} \varphi_{i,L} P n_{1M} dA_e$ (320)

$\displaystyle \{F\}_{(i)}$ $\displaystyle = [K_{PA}]_{e(i)(jM)} \cdot \{A\}_{(jM)} + [K_{PP}]_{e(i)(j)} \cdot \{P\}_{(j)}$
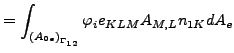$\displaystyle = \int_{{(A_{0e})}_{\Gamma _{12}}} \varphi_i e_{KLM} A_{M,L} n_{1K} dA_e$
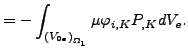$\displaystyle = - \int_{{(V_{0e})}_{\Omega _1}} \mu \varphi_{i,K} P_{,K} dV_e.$ (321)

これらは外力と釣り合わなければなりません。

以上の理論は実際のモデリングに関して何を意味するのでしょうか？　駆動電流の流れる伝導体はシェル要素を使ってモデル化しなければならないのです。シェル要素の厚みはさまざまに変えることができます。電流は通常表面近くを流れる（表皮効果）ので、シェル要素でのモデリングはたいした制約にならないのです。伝導体の電流とポテンシャルは熱伝達と同様の方法で計算されます。つまりポテンシャル境界条件は温度の様に、電流境界条件は熱流条件の様に定義されねばならないのです。伝導体を流れる駆動電流は磁場や電場の計算に使用されるメッシュとは完全に切り離されています。駆動用電磁コイルの電流はそれによって生成される電磁場によは影響されないということに注意してください。

問題となる体積領域は Ω1 、Ω2 、Ω3 です。これら3つの領域は空気、伝導試料、試料材料が空洞でない場合に試料を単連結にする空気の一部です。これら3つの両機は体積要素によってメッシュ化されます。メッシュは接続している必要はなく、それぞれ完全に異なるやり方で領域をメッシュ化することも可能です。同様に各領域に対してそれぞれ適切なメッシュ粗密を設定することもできます。

駆動電流に基づいてビオ・サバール則を使用して領域1の場 T0 が決定されます。ビオ・サバールの積分は計算的に非常に負荷が高いため、この部分のコードは並列化されています。また式（318）から、領域1と接する領域2・領域3の外部面での T0 も決定されます。

以下の境界条件が（MPCを通して）課されます。

領域2または領域3に接する領域1の外部面上での

領域1に接する領域2と領域3の外部面での

領域2と領域3の間の面での

これらMPCは CalculiX によって自動的に生成されるのでユーザーは特に注意する必要はありません。また最後に V の値が領域2の少なくとも1点で固定されなければなりません。これは自由度 8 に対して *BOUNDARY 条件を使ってユーザーによって行われる必要があります。

定義されるべき材料データは以下の通りです。

これらは*DENSITY、*CONDUCTIVITY、*SPECIFIC HEAT、*ELECTRICAL CONDUCTIVITY、MAGNETIC PERMEABILITYカードを使って設定できます。熱輻射が存在する場合には *PHYSICAL CONSTANTS も必要です。

プロシージャ・カードは *ELECTROMAGNETICS です。静磁気計算では MAGNETOSTATICS パラメーターを、熱無しの電磁気計算では NO HEAT TRANSFER を使用します。デフォルトでは熱伝達ありの電磁気計算になります。

使用可能な出力変数は *NODE FILE カードの POT（駆動電流コイルの電気ポテンシャル）と *EL FILE カードの ECD（駆動電流コイルの電流密度）、EMFE（試料の電場）、EMFB（空気と試料の磁場）です。サンプルは induction.inp と induction2.inp になります。

次へ 上へ 前へ 目次へ
次へ：Convergence criteria 上へ：Types of analysis 前へ：Substructure Generation 目次へ
guido dhondt 2016-03-08